算法与数据结构--空间复杂度O(1)遍历树

冬天已经来了，秋招早已悄无声息的结束。作为一个已经工作了两年的老人，校招面试感觉就像高考一样遥远。但是呢，虽然工作了，还是要时刻保持危机感的呀，万一哪天就要跳槽了呢(￣∇￣)。

遥想当年面试的时候，由于没有学过数据结构，在面试官出算法题之前就老实交待家底：“我的算法和数据结构不太行，树呀图呀都不太会(✿◡‿◡)"。但是经过两年断断续续的学习，发现其实树是一个套路非常明显的一类算法题，而遍历树是解决绝大多数树问题的基础（很多题目都是在树的遍历上扩展），下面小鹿就以树的遍历为例，解剖树里面深深的套路吧o(*￣▽￣*)o。

树的基础回顾

二叉树长什么样子，小鹿这里就不上图啦，所谓的根节点、叶子节点也不介绍啦。我们知道，二叉树的遍历分为三种：前序、中序和后序。这三种序的不同主要就是在于什么时候访问根节点。以前序为例，在遍历一颗树的时候先访问根节点，再遍历其根节点的左子树，最后访问根节点的右子树。而中序遍历就是先遍历左子树，再访问根节点，最后遍历右子树；后序遍历小鹿就不重复啦。

树的递归

树有一个很好的特性，就是一棵树的根节点的左右子树仍然是一颗树

这好像是一句正确的废话╮(￣▽￣"")╭

所以我们可以把一棵复杂的大树，分解成两颗稍微小一点的树，依次类推，最后变成最小的单元（只有一个节点的树）。不管怎么讲，处理只有一个节点的树是不是超级容易！！！这个呢就是递归的思想，所以说到这里，我们以后只要遇到关于树的问题，谁还不会用递归走一波呢！

下面就来开始实践！用递归的思想实现二叉树的前序、中序、后序遍历（遍历结果记录在self.ans的向量里）。小鹿这里就用python写啦（真的不要纠结编程语言噢）。遍历一个有n个节点的树，其时间复杂度和空间复杂度都是O(n)。

树和栈

用递归的思路解决树的遍历或者其他树的问题，思路非常清晰，代码也会非常的简单清楚。当我们在使用递归（函数的嵌套）的时候，其本质是在调用栈。我们可以用栈来实现树的遍历，进一步理解递归的思想。

用栈来实现树的遍历就稍微复杂一点啦。首先前序是最简单的，我们用一个栈（first-in-last-out）来维护树遍历的顺序。初始状态是把非空的根节点push到栈中，逐个从栈中取出节点，访问其值，然后先push右节点再push左节点到栈中，就保证访问顺序是 root->left->right 啦。超级简单有木有！

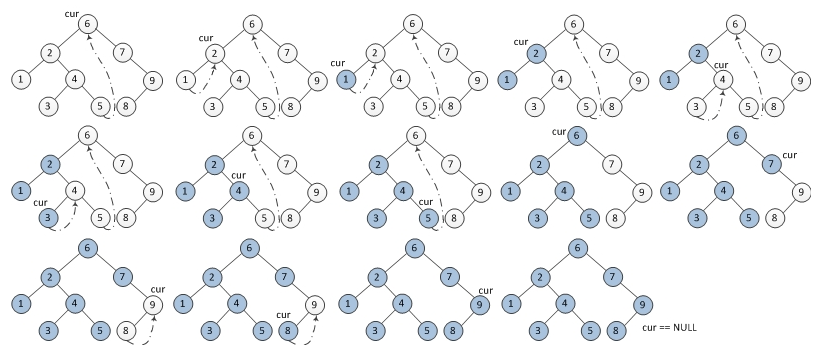
中序遍历就稍微难一些了，在访问一个节点之前需要访问其 left-most 节点，将其左节点逐个加入到栈中，直到当前节点为None。然后从栈中取出节点，由于栈的特性，在取出某个节点之前，其左节点已经被访问，所以就可以安心的访问该节点，然后把当前节点置为其右节点，依次类推。

后序遍历和中序遍历差不多，在中序遍历的基础上需要增加一个prev记录上一个访问的节点，确认在访问某个节点之前其右节点是否已经被访问。

用栈的方式遍历树，更加显式的告诉了大家树遍历的时候是怎么回溯的，其时间空间复杂度仍然是O(n)。

Morris遍历

下面小鹿要给大家介绍一个神级树遍历方法Morris，使其空间复杂度从O(n)变成O(1)!

树的遍历一个难点就是确定什么时候以及回溯如何回溯（好像是两个点），第一种递归的方法通过函数的嵌套实现回溯，第二种方法通过栈存储节点的顺序实现回溯，而Morris则是利用树中空节点记录每个节点其回溯的节点，实现空间复杂度为O(1)的遍历。

具体来说，当我们访问了某个左子树最右的节点后需要回溯到其左子树的根节点，但是怎么回去呢，我们需要在之前加一个链接，将该根节点连到其左子树的最右节点的右节点上。是不是有点绕呢(╯﹏╰)b，不慌！小鹿带你一起做一遍中序遍历的例子就清楚啦~~

以上面的图为例做中序遍历，当前节点为6（curr=6）时，找到其左子树的最右节点5，添加链接备用，这样从节点5我们就可以回溯到节点6。更新当前节点，curr=2，重复相同的操作。当curr=1时，到达叶子节点，输出(节点变蓝)，因为之前添加了链接，所以可以从节点1回溯到节点2，回溯删除链接。当前节点变成4，以此类推下去

已经懵逼的小伙伴们请仔细品味下面的代码(￣▽￣)～

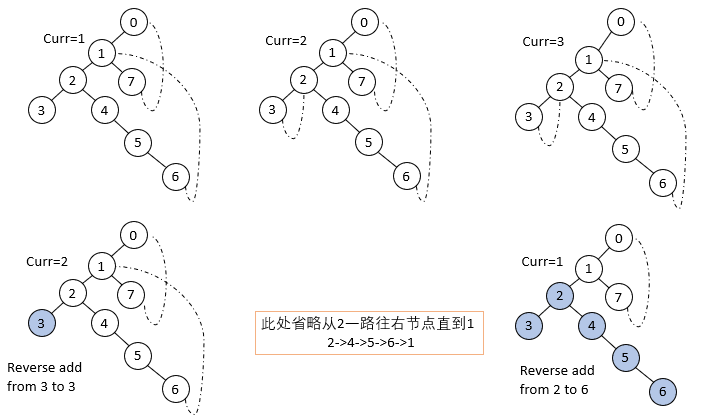
Morris前序遍历和中序遍历几乎一模一样，唯一的差别就是在第一次访问节点的时候就输出，还是第二次访问节点的时候输出。Morris后序遍历在此基础上还要稍微的复杂一丢丢。因为后续遍历根节点最后输出，需要增加一个dump节点作为假的根节点，使其的左子树的 right-most 指向原来的根节点。话不多说，我们来看下代码吧！

眼尖的小伙伴看了代码之后就会发现，Morris后序遍历怎么多了两个函数，怎么和前序和中序不一样了呢ヽ(`Д´)ﾉ！这个Morris后序遍历确实比较挺难理解，我们还是用最简单的图示来走一遍代码的意思吧~~~

开始除了加了一个dump节点以外，都是一样的一路向下，到达left-most节点3，不输出（注意啦！不一样啦！）然后回溯到节点2，逆序输出从3到3的节点，删除链接。从节点2一路往右回溯到节点1，逆序输出从其左节点2到prev节点6，删除节点。以此类推，就噢啦ヽ(￣▽￣)ﾉ。

现在大家都清楚了吧~~不清楚的地方欢迎在评论区提出噢，小鹿会尽最大努力为大家答疑解惑嗒(￣▽￣)／后面小鹿鹿鹿还会持续推送关于算法和数据结构的小文章，大家有兴趣的话欢迎关注订阅哦(´▽`)ﾉ 。

感谢大家的阅读[]~(￣▽￣)~*（鞠躬）