在了解Markov Processes之前呢,我们先来介绍一下马尔科夫性质。
具有马尔科夫性质的状态满足下面公式:
根据公式也就是说给定当前状态St,将来的状态与t时刻之前的状态已经没有关系。
如下图解释:
其中:
* St状态能够捕获历史状态的相关信息
* 一旦当前状态已知St,历史可以被忽视
State Transition Matrix
可以用下面的状态转移概率公式来描述马尔科夫性:
下面状态转移矩阵定义了所有状态的转移概率:
其中的每行和为1.为什么每行和为1。我们可以举一个例子,比如我们掷骰子游戏,当前的点数为1,那么我们再一次掷骰子得到的点数的概率是多少呢?
对应于上面转移概率来说,即使我们不知道下一个具体点数的概率,但是我们至少知道下一个点数是1,2,3,4,5,6中的某一点,那么就会有:
这就解释了为什么每行和为1。
Markov Process
马尔科夫过程一个无记忆的随机过程,是一些具有马尔科夫性质的随机状态序列构成,可以用一个元组<S,P>表示,其中S是有限数量的状态集,P是状态转移概率矩阵。如下:
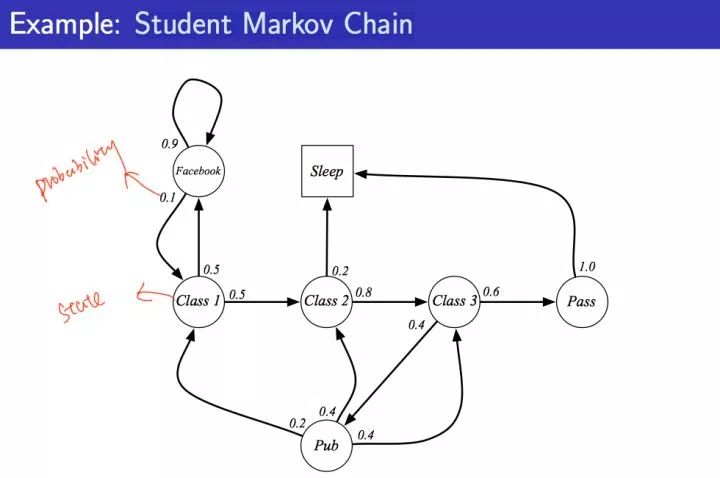
学生马尔科夫链这个例子基本贯穿了本讲内容:
图中,圆圈表示学生所处的状态,方格Sleep是一个终止状态,或者可以描述成自循环的状态,也就是Sleep状态的下一个状态100%的几率还是自己。箭头表示状态之间的转移,箭头上的数字表示当前转移的概率。
举例说明:当学生处在第一节课(Class1)时,他/她有50%的几率会参加第2节课(Class2);同时在也有50%的几率不在认真听课,进入到浏览facebook这个状态中。
在浏览facebook这个状态时,会有90%的几率在下一时刻继续浏览,也有10%的几率返回到课堂内容上来。
当学生进入到第二节课(Class2)时,会有80%的几率继续参加第三节课(Class3),也有20%的几率觉得课程较难而退出(Sleep)。
当学生处于第三节课这个状态时,他有60%的几率通过考试,继而100%的退出该课程,也有40%的可能性需要到去图书馆之类寻找参考文献,此后根据其对课堂内容的理解程度,又分别有20%、40%、40%的几率返回值第一、二、三节课重新继续学习。
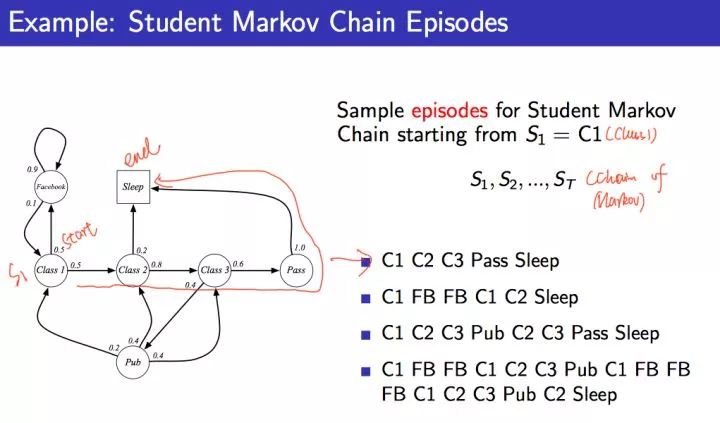
一个可能的学生马尔科夫链从状态Class1开始,最终结束于Sleep,其间的过程根据状态转化图可以有很多种可能性,这些都称为Sample Episodes。比如下面四个Episodes都是可能的:
我们可以使用采样技术来sample一些Episodes。
slides如下:
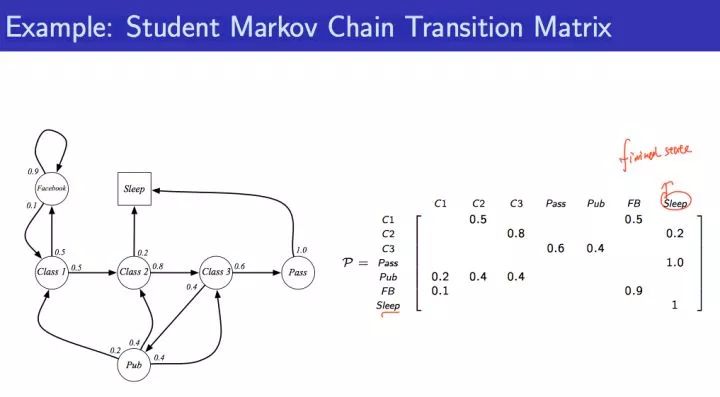
该学生马尔科夫过程的状态转移矩阵如下图:
今天暂时总结到这,下次将总结Markov Reward Processes、Value function等知识点哦,敬请期待~
希望对大家的理解有帮助~欢迎大家指错交流!
参考:
David Silver深度强化学习课程 第2课 - 马尔科夫决策过程
知乎专栏:叶强:《强化学习》第二讲 马尔科夫决策过程
本篇文章来源于: 深度学习这件小事
本文为原创文章,版权归知行编程网所有,欢迎分享本文,转载请保留出处!


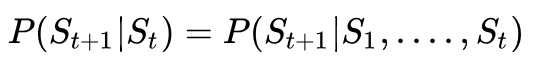

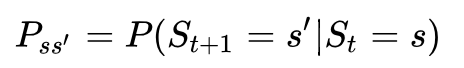
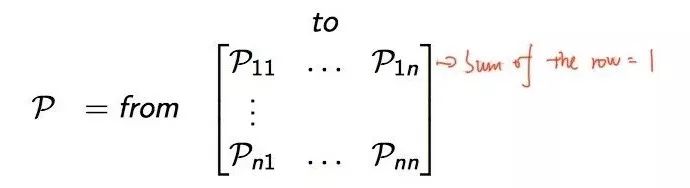
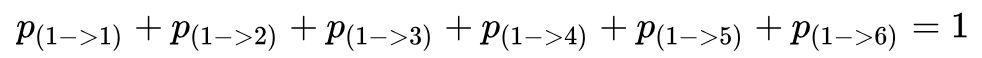




内容反馈