继上篇通俗易懂讲解感知机(二)--学习算法及python代码剖析感知机学习算法以及python实现讲完之后,其实感知机的知识大部分已经讲完,这篇文章可以收尾一下,讲解一下感知机的对偶形式,以及证明一下为什么在迭代有限次的时候可以收敛等知识。
下文目录如下:
1.感知机学习算法的收敛性证明
2.感知机学习算法的对偶形式
3.为什么引出引出对偶形式
4.对偶形式python代码讲解
5.感知机内容的总结
推荐阅读方式:
结合前面讲过的通俗易懂讲解感知机(一)--模型与学习策略、通俗易懂讲解感知机(二)--学习算法及python代码剖析以及李航博士的《统计学习方法》一起阅读,效果较好!
1
感知机学习算法的收敛性
我们需要证明经过有限次迭代可以得到一个将训练数据集完全正确划分的分离超平面及感知机模型。(证明了,我们心里才有底,否则都不知道是否能够保证收敛)
我们会有以下定理:
设训练数据集T={(x1,y1),(x2,y2),...,(xn,yn)}是线性可分的,则下面俩个定理成立:
由上面定理可以得到,直白来说,如果是一个线性可分的数据集,我是可以在有限次k更新,得到一个将数据集完美分割好的超平面(感知机模型)。
下面给出证明:(前方数学证明预警,这里默认收敛性成立也是可以的,不影响应用)
定理一证明如下:
定理二证明如下:
友情提示,可能不是太清楚,但是只要仔细跟着去看,一定能够看懂。把收敛性的证明该注意的地方全部写到了。(完全按李航博士书籍顺序讲解)
那么我们可以得到结论,误分类的次数k是有上界的,当训练数据集线性可分的时候,感知机学习算法原始迭代是收敛的!(证明了算法是对的,可行的)
2感知机学习算法的对偶形式
对偶形式就是将参数w,b表示为实例xi和标记yi的线性组合的形式,通过求解其系数而求得w和b,对误分类点进行更新,我们假设初始值w0,b0均为0,对误分类点(xi,yi)通过:
这里,αi当η=1的时候,它就表示第i个实例点由于误分而进行的更新的次数,实例点更新次数越多,意味着它距离分离超平面越近,也就越难正确分类(越容易分错,超平面一动不多就容易将这些点分错),换句话说,这样的实例对学习结果影响最大(在支持向量机中,这些点代表着支持向量)
那么我们怎么得到它的对偶形式呢?将xi,yi表达的w带入原来感知机模型中,得到下面对偶感知机模型:
根据上面模型方程,我们可以看出与原始感知机模型不同的就是w的形式有所改变,那么到底为什么有对偶形式出现了,后面会讲原因!
得到下面的对偶形式算法学习步骤:
这里的更新说明如下:
αi = niη 则 αi+1 = αi + η
推出
ni+1η = niη + η 则 ni+1 = ni + 1
代表的意思为该点如果分错,那么更新次数加一,b的更新方式与原感知机模型更新方式一样。
3为什么要引出对偶形式
根据查阅资料,普遍的观点是以下两点:
1.从对偶形式学习算法过程可以看出,样本点的特征向量以内积的形式存在于感知机对偶形式的训练算法中,凡是涉及到矩阵,向量内积的运算量就非常大(现实中特征维度很高),这里我们如果事先计算好所有的内积,存储于Gram矩阵中,以后碰到更新的点,直接从Gram矩阵中查找即可,相当于我就初始化运算一遍Gram矩阵,以后都是查询,大大加快了计算速度。
2.跟SVM的对偶形式其实有类似之处(后面讲到SVM的时候再说明)
对偶形式python代码讲解
根据算法过程,有以下步骤:
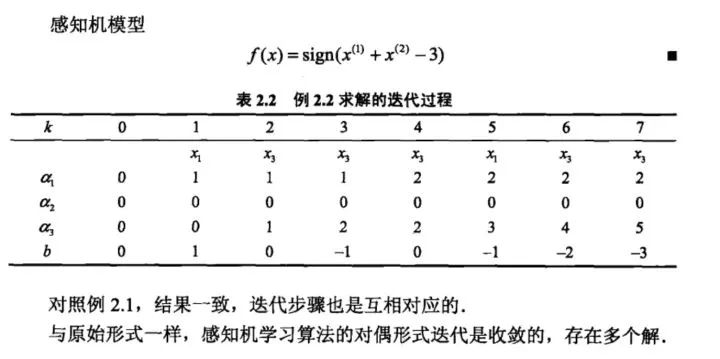
最终我们可以将迭代过程中的参数变化写出如下表所示:
有了算法逻辑流程,代码很简单,下面我们根据这个例子写出python代码如下:
分开讲解:
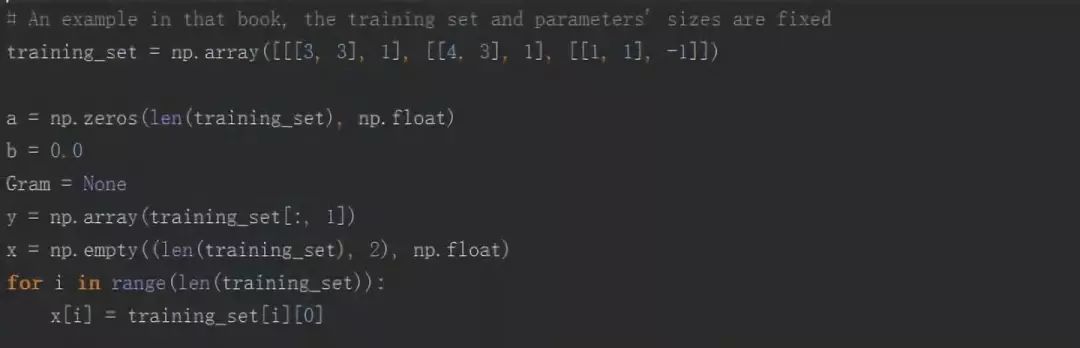
首先我们初始化和处理数据,代码如下:
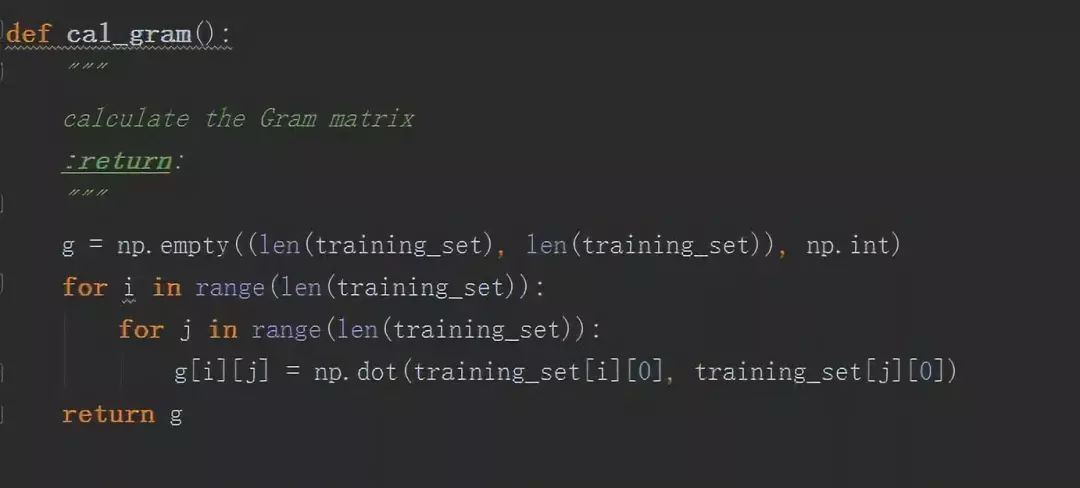
获得Gram矩阵,代码如下:
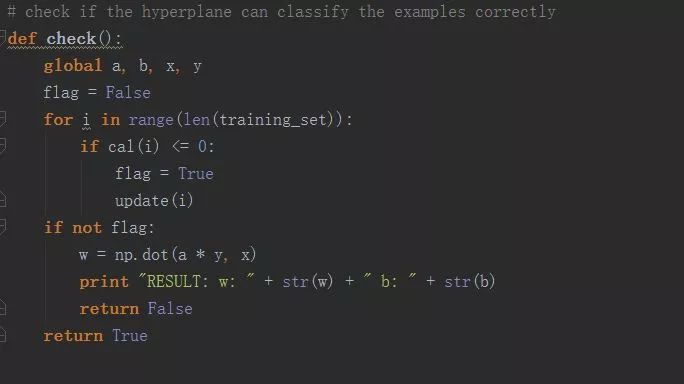
检查所有分类点是否分类正确:
按照公式更新参数:
主函数控制逻辑以及控制迭代次数:
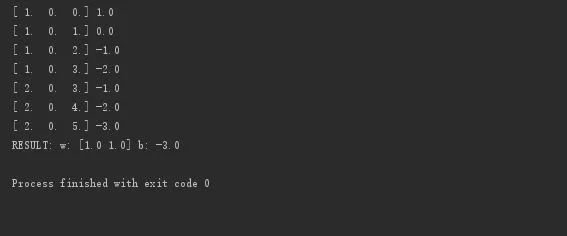
代码结果如下:
与我们例子中是完全对应的!
完整代码如下:
<span style="color: #cc7832;">import </span>numpy <span style="color: #cc7832;">as </span>np# An example in that book, the training set and parameters' sizes are fixed
training_set = np.array([[[3, 3], 1], [[4, 3], 1], [[1, 1], -1]])
a = np.zeros(len(training_set), np.float)
b = 0.0
Gram = None
y = np.array(training_set[:, 1])
x = np.empty((len(training_set), 2), np.float)
for i in range(len(training_set)):
x[i] = training_set[i][0]
def cal_gram():
"""
calculate the Gram matrix
:return:
"""
g = np.empty((len(training_set), len(training_set)), np.int)
for i in range(len(training_set)):
for j in range(len(training_set)):
g[i][j] = np.dot(training_set[i][0], training_set[j][0])
return g
def update(i):
"""
update parameters using stochastic gradient descent
:param i:
:return:
"""
global a, b
a[i] += 1
b = b + y[i]
print a,b
# calculate the judge condition
def cal(i):
global a, b, x, y
res = np.dot(a * y, Gram[i])
res = (res + b) * y[i]
return res
# check if the hyperplane can classify the examples correctly
def check():
global a, b, x, y
flag = False
for i in range(len(training_set)):
if cal(i) <= 0:
flag = True
update(i)
if not flag:
w = np.dot(a * y, x)
print "RESULT: w: " + str(w) + " b: " + str(b)
return False
return True
if __name__ == "__main__":
Gram = cal_gram() # initialize the Gram matrix
for i in range(1000):
if not check(): break
5感知机内容总结
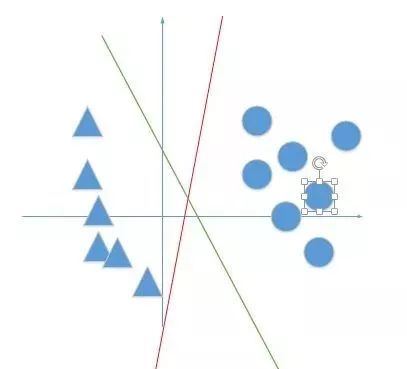
1. 感知机是一个二分类学习算法,是后面神经网络与支持向量机的基础。它着重考虑是否将所有训练数据分类正确,而不考虑分的有多好,这是与支持向量机所不同的地方。如图所示:
在感知机看来,红色与绿色的模型是一样好的,但是支持向量机看来,绿色的模型要比红色的模型要好。
2.感知机模型中,只要给出的数据是线性可分的,那么我们就能证明在有限次迭代过程中,能够收敛(有了它,我们心里才有底,保证了算法正确性)
3. 感知机有它的对偶形式,其实与原始形式很多地方是一样的,对偶形式的出现为后面支持向量机的对偶形式打了基础,Gram矩阵的出现也大大减少了我们的计算量!
好,到这里为止,讲完了第一章感知机的相关知识!希望对大家有帮助,欢迎大家指错交流!
参考:
李航《统计学习方法》
致谢:
郭江师兄,晓明师兄,德川,皓宇,继豪,海涛师兄
推荐阅读:
通俗易懂讲解感知机(一)--模型与学习策略
通俗易懂讲解感知机(二)--学习算法及python代码剖析
本篇文章来源于: 深度学习这件小事
本文为原创文章,版权归知行编程网所有,欢迎分享本文,转载请保留出处!
你可能也喜欢
- ♥ 时间序列预测方法总结06/05
- ♥ 这5种动态炫酷图,用Python就可以画!05/22
- ♥ MIT牛人解说数学体系05/26
- ♥ 如何防止我的模型过拟合?这篇文章给出了 6 大必备方法07/31
- ♥ FLAT:中文NER屠榜之作!01/23
- ♥ 中国顶级 AI 研究者数量仅为美国 1/5:美国智库最新全球 AI 实力报告04/05





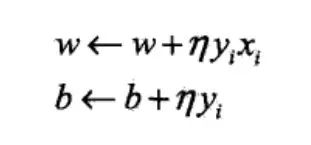
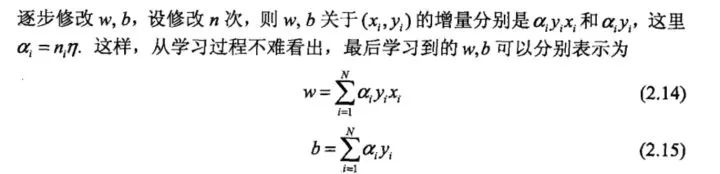

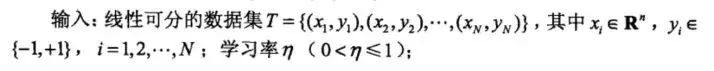



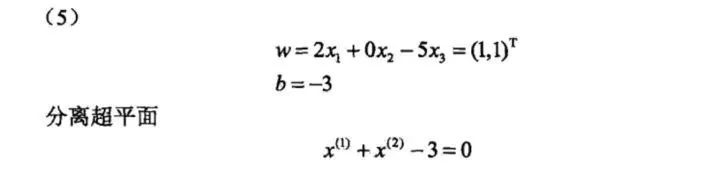




内容反馈