从小到大，数学都是一门令人头秃充满魅力的学科。从基本的代数、几何，到高数微积分，各类数学问题都对答题者的逻辑推理能力都有着不同程度的挑战。

而逻辑推理能力一直以来都是 AI 发展的核心目标之一。学术界对于 AI 自动解数学题的研究也已有时日。由于数学题对于各类复杂逻辑推理能力的要求，该任务往往可以作为一个很好的基准，用以评估 AI 的智能化水平。

但近年来的相关研究还是局限在数学应用题（MWPs）上。任务难点集中在如何把文字形式的问题描述，转换为数学化的推理过程。任务难度还是很高的，毕竟咱真人也没有做得特别好 (:з」∠)

可以看到，之前工作研究的这类数学题都只涉及文字形式的问题描述，整个过程是“单模态”的。但我们从小到大积攒的丰富刷题经验告诉我们：不是所有数学题都是“单模态”任务，还有一类题，是要看图说话的！我们称之为，几何题。

今天介绍的这篇 ACL'21 Finding 的论文，就在此前工作的基础上又往前进了一步，探究了如何使得 AI 自动化解答几何题。与之前的单模态问题相比，几何题的解答有以下几点全新的挑战：

• 图表中蕴含很多文本中不具备的复杂信息，比如点、线的相互位置关系，模型需要充分地解析图表信息。
• 模型需要同时理解文本和图表，并进行跨模态的数值推理。
• 题目中还涉及一些知识点（如勾股定理）的运用，模型需要学会运用这些知识。

也就是说，几何题的解答是一个 多模态数值推理 的过程。它同时包含了多模态与逻辑推理 两大热点研究主题，值得关注一下。

论文标题：
GeoQA: A Geometric Question Answering Benchmark Towards Multimodal Numerical Reasoning

论文链接:
https://arxiv.org/abs/2105.14517

GitHub链接:
https://github.com/chen-judge/GeoQA

GeoQA基准

由于之前已有的几何题数据集规模极小，只有大概200题。这篇文章先从数据集入手，提出了 GeoQA 数据集，共有5010道几何题，标注了丰富的题目信息，包括题目描述、题目类型、运用的知识点和解题的过程。

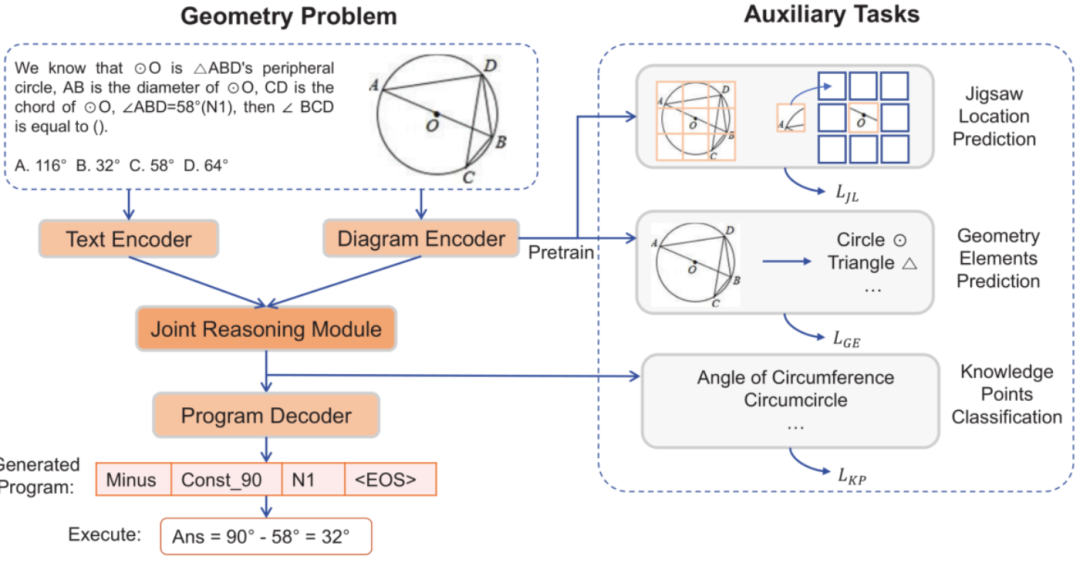
为了规范化对解题过程的描述，该文设计了一系列所谓程序语言(program)，包括一些基本操作OP、常数Const、题目变量N、过程变量V。而这些program可以直接被计算机一步一步地执行，计算出一个最终的答案。比如在图一中，(PythagoreanMinus, N0, V0) 就代表利用勾股定理和相减操作，对题目中出现的半径长度5(N0)与上一步执行得到的OE长度3(V0)进行运算，求得AE的长度为4(V1)。

也就是说，program可以作为一个桥梁，把人类的解题过程转化为计算机更容易理解的程序语言。这样神经网络模型就可以通过预测这些program，来做出可解释的数值推理。

NGS模型

在方法部分，文章提出了一个用于解决几何问题的神经网络模型Neural Geometric Solver (NGS)，对几何题的多模态数据进行建模：

• 首先使用两个编码器，分别对文本和图表信息进行编码
• 使用一个基于协同注意力机制(co-attention)的推理模块来融合文本和图表的表征
• 基于上一步得到的跨模态融合表征，模型用解码器直接预测出可执行的program序列。

前文也有提到过，几何题存在如何充分解析图表信息以及如何运用定理知识的挑战。所以该工作，又提出了三个辅助任务，来增强NGS的语义表征能力。这三个任务分别是：拼图位置预测、几何元素预测和知识点预测。

前两个任务是为了强化图表编码器的。由于模型里图表编码部分用的是ResNet，预训练时使用的都是一些自然图像，和我们研究的几何题图表还是有很大差异的。所以很自然地想到了，用自监督的方式来训练一个更好的图表编码器，包括拼图位置预测和几何元素预测。

拼图位置预测是把图表划分成3x3片区域，再打乱各片区域的顺序，并让模型去测它们的相对位置关系，借以增强图表编码器对图表信息的理解。几何元素预测则是让模型去预测图表中出现的几何元素，比如三角形、圆形等等，也可以起到增强图表编码器的作用。

第三个辅助任务，知识点预测，训练模型去预测每道题对应的知识点，旨在使模型能够更加准确地运用定理知识。整个数据集共涉及50个知识点，而每个问题包含一至多个知识点，因而这个预测过程也就是一个多标签分类问题。

实验

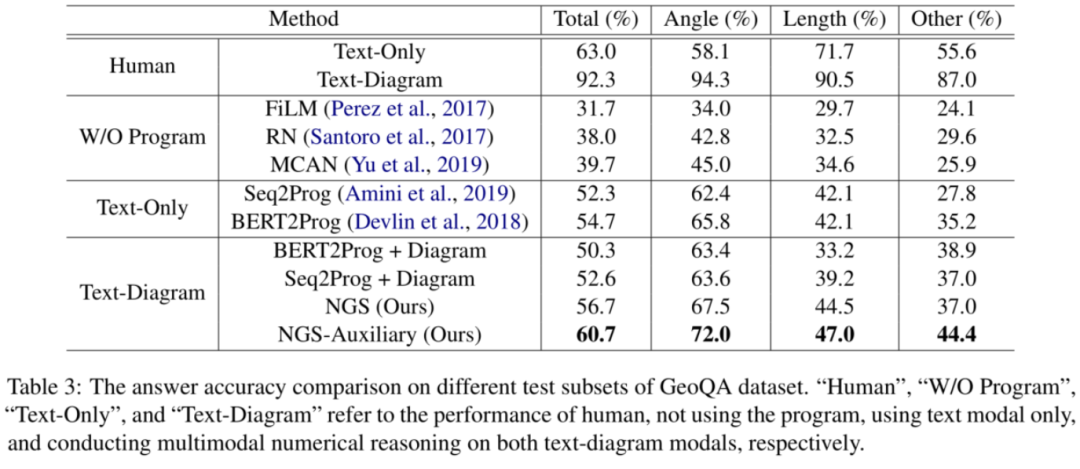
下图是一些主要的实验对比结果及分析。其中，

• Human代表的是人类水平，是由十个很擅长几何题的学生做出来的结果。神经网络模型与之仍有很大差距，在未来还有很大的研究空间。
• W/O Program指的是不使用文章定义的一系列program来规范化描述解题过程，而直接用分类的方式预测结果。这一类中的三个baseline是一些在VQA任务上的隐式推理模型。这类模型的性能普遍比较低，证明了program定义的必要性。
• Text-Only是只使用文本模态求解几何题。性能较差，说明了在几何题上进行多模态推理的必要性。
• Text-Diagram同时使用文本和图表。相比于一些简单的融合方法，本文的NGS模型取得了最好的性能。

也有 Ablation Study， 分析了本文提出的各个辅助任务的具体效果。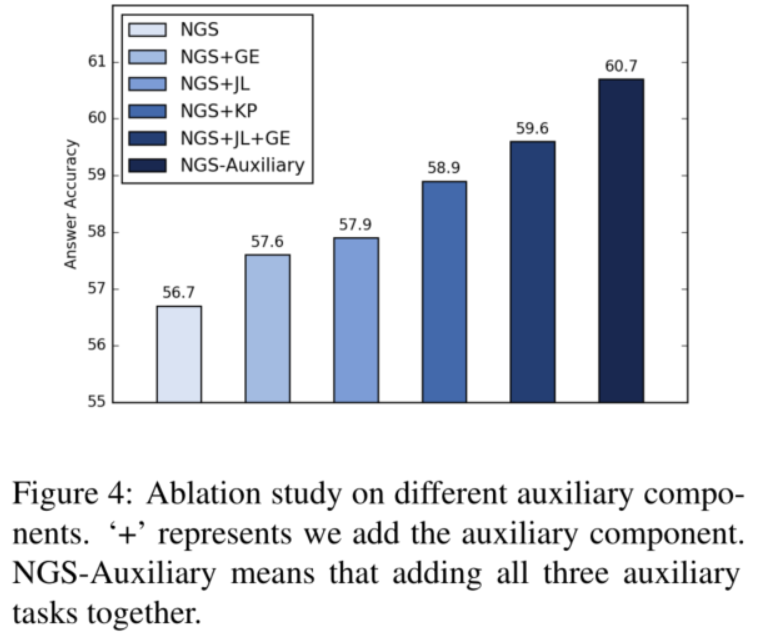

总结

本文首次探究了 AI 自动化解答几何题任务，搜集了大规模的几何题问答数据集GeoQA，并基于定义的program对该数据集进行了人工标注，帮助模型去理解、预测程序化的解题过程。此外，本文提出NGS模型以建模几何题多模态信息，并引入了多个辅助任务，来提升其在几何题问答任务上的性能表现。

几何题解答任务涉及了多模态、逻辑推理等多个当今热点研究主题，值得关注。或许在未来，AI 也能学会自己解题，甚至充当智能教师，给教育行业带来一场颠覆性的智能变革。