知行编程网知行编程网  2022-05-12 16:00 知行编程网 |  隐藏边栏 |   抢沙发 |  28 
文章评分 0 次，平均分 0.0 ：

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量

来自 | arXiv   作者 | Rohan Anil等

转自 | 机器之心编译
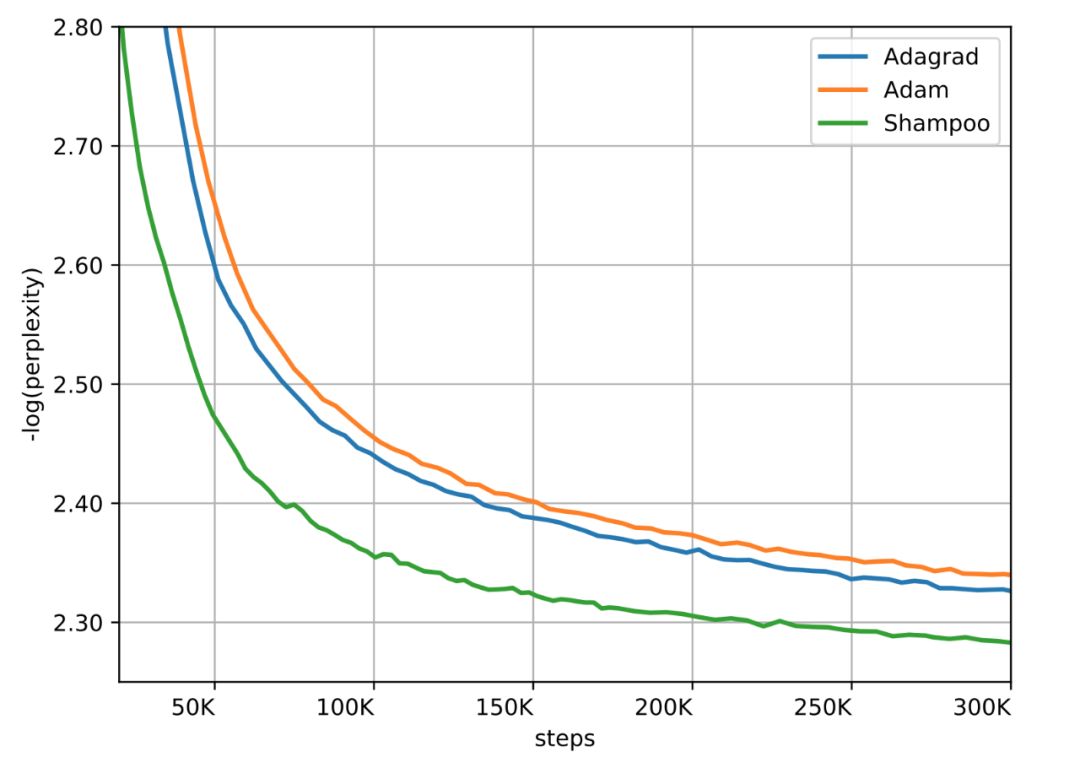
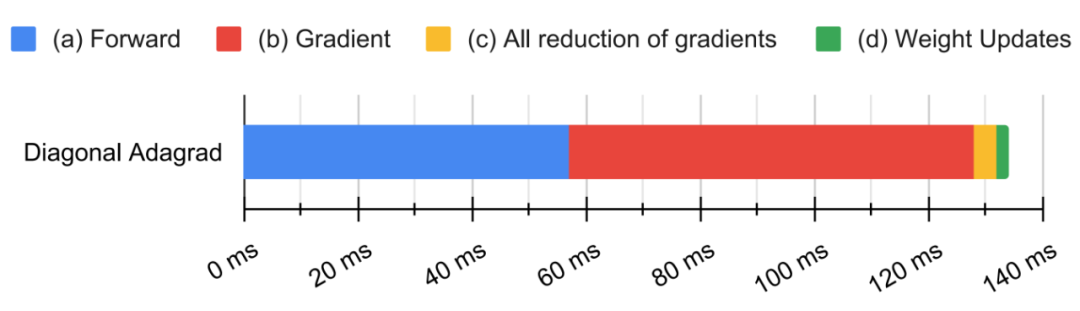
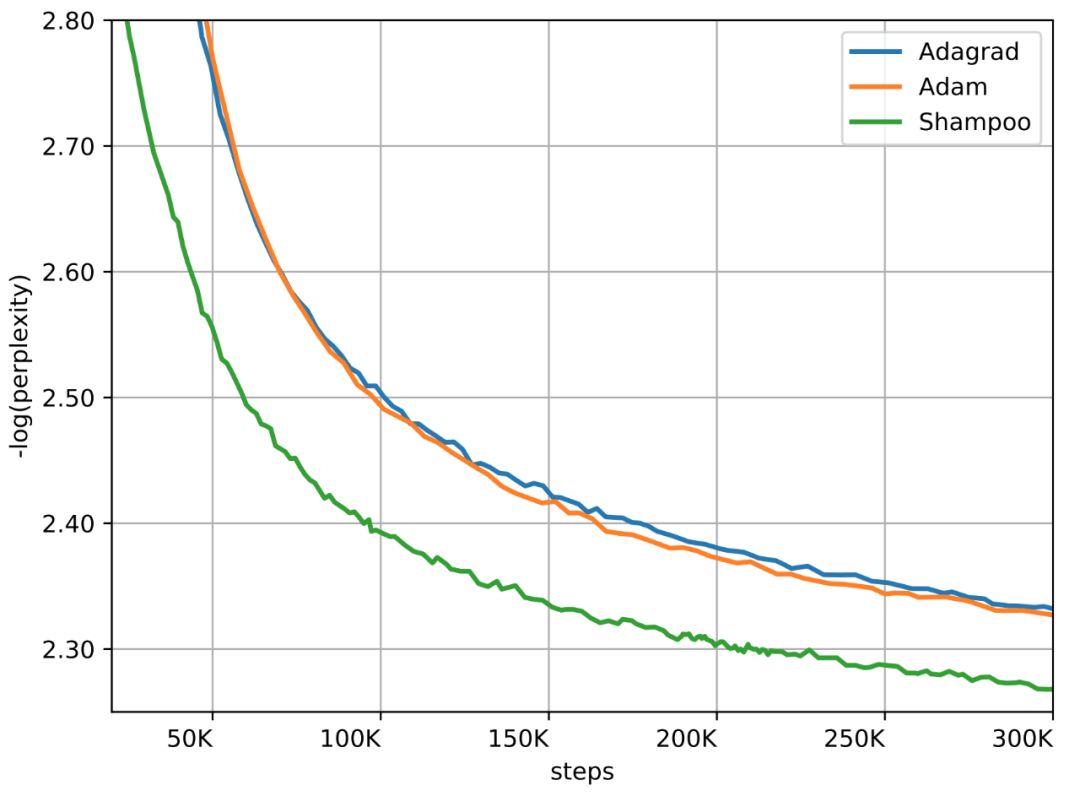
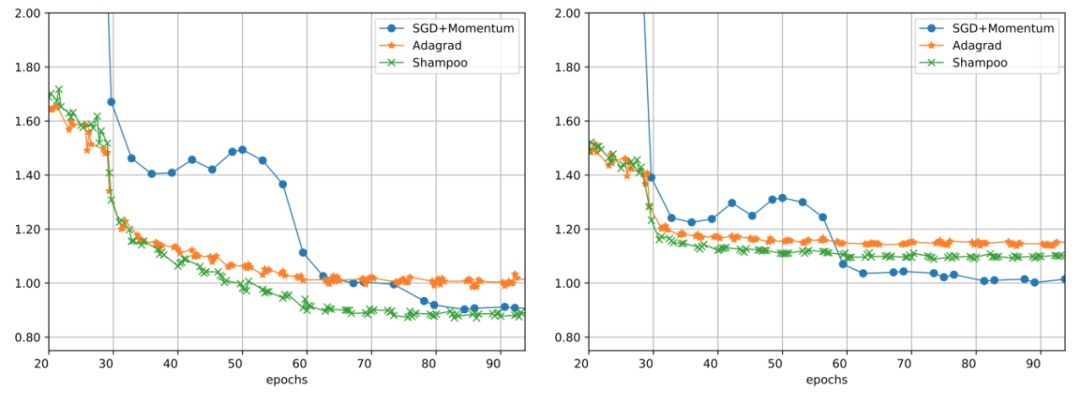
常见的最优化器，如 Adam、AdaGrad、SGD+Momentum 等，都是一阶的。但是二阶梯度的收敛速度相比它们就快了太多。近日，谷歌研究者联合普林斯顿大学等，提出了真正应用的二阶梯度最优化器 Shampoo，让这个理论上颇有前景的设想变为现实。
二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量

目前，无论是从理论还是应用层面来说，机器学习中的优化都是以随机梯度下降等一阶梯度方法为主。囊括二阶梯度和/或二阶数据统计的二阶优化方法虽然理论基础更强，但受限于计算量、内存和通信花销等因素，二阶梯度优化方法的普及度不高。

可能你用各种框架搭建过各种神经网络，同时也尝试过调用 Adam、AdaGrad、SGD+Momentum 等形形色色的最优化器。但是你会发现，它们都采用一阶梯度，二阶梯度似乎仍然遥遥无期。

然而在谷歌大脑与普林斯顿大学等研究者的努力下，二阶梯度优化终于在实战大模型上展现出独特的优势。

研究者表示，为了缩短理论和实际优化效果之间的差距，该论文提出了一种二阶优化的概念性验证，并通过一系列重要的算法与数值计算提升，证明它在实际深度模型中能有非常大的提升。

论文地址：https://arxiv.org/abs/2002.09018

具体而言，在训练深度模型过程中，二阶梯度优化 Shampoo 能高效利用由多核 CPU 和多加速器单元组成的异构硬件架构。并且在大规模机器翻译、图像识别等领域实现了非常优越的性能，要比现有的顶尖一阶梯度下降方法还要好。

我们可以先看看它在 WMT 英-法翻译数据集上的效果，它采用的是标准的 Transformer。除了这一个实验，研究者还测试了 Big Transformer 以及 ImageNet 上的 ResNet，这些实验结果都展示在后文中。

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量
WMT'14 英法翻译数据集上的 Transformer，二阶梯度算法 Shampoo 在迭代数上快了 1.95 倍，且就算要计算二阶梯度，每一次迭代也只慢了 16%，总体上来说节省了 40% 的执行时间。

从上图可以清楚地看到，如果 Adam 和 Shampoo 要训练到相同的准确度，Adam 需要迭代 30 万次，而 Shampoo 大概只需要迭代 11 万到 12 万次就差不多了。二阶梯度，果然收敛速度快了太多。

二阶梯度是什么

想象一下，如果我们希望找到「谷底」，那么沿着坡度一步一步往下走就行了。对于机器学习来说，「谷底」就是最优解，一步一步就是迭代过程。之前，我们采用一阶梯度，也就是坡度的陡和缓来确定步子要迈多大。而当坡度是有变化的，即逐渐变陡或变缓，根据当前坡度来确定步子大小就有一些问题。

之前我们可以慢慢多走几步，就能根据坡度的变化直接调整。现在如果能用二阶梯度，相当于梯度的梯度，那么也就知道坡度变化的趋势，因此一步就能走到位。所以二阶梯度本质上比一阶梯度多出一些信息，模型收敛也就会更快。

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量
对于凸优化，二阶梯度一次就能找到最优解，而一阶梯度找到的方向必定垂直于当前点的等高线，因此出现这种「锯齿」现象。

二阶梯度策略无疑是数学优化中性能最有保障的算法之一。在这种算法中，我们使用预条件算子（preconditioner）矩阵转换梯度，然后应用到每个迭代步骤上。一般来说，这包括计算/近似估计二阶导矩阵，如 Hessian。另一方面，AdaGrad 和其他相关的算法主要针对随机优化，使用二阶梯度的方差矩阵来构建预条件算子。

虽然二阶方法在收敛性上比一阶好很多，但是其计算量限制了实际的应用。因为在每次梯度更新的时候，这种算法需要平方级别的存储和立方级别的计算时间。因此，这些方法在现在的机器学习优化方法中并不常见。

现代优化策略面对的最大的一个挑战是在理论和实际优化方法中搭建一个桥梁，使得二阶优化方法能够更合理地被应用和部署。

在这篇论文中，研究者真正提出了一种二阶梯度改进方法，它与 Adam 等算法一样是适应性梯度，但它能利用二阶梯度信息加速收敛，甚至在大型机器翻译模型中收敛快了一半。

二阶梯度，超越 Adam 的最优化

为了完成这项工作，研究者仔细思考了二阶优化存在的问题与困难，并改进了名为 Shampoo 的二阶梯度方法。研究者表示，二阶优化最无解的是目前深度学习库对一阶梯度已经有了大量优化，它们对计算量与内存的要求都不高。然而，对于 Shampoo，每一次迭代的密集计算，都对应用大模型产生了不可逾越的阻拦。

和一阶梯度优化方法相比，Shampoo 要走向实践，还有如下三大挑战。

1. 算法上的挑战

现代机器学习架构通常使用很大的嵌入层，维度可能多达百万级别。Shampoo 需要对每个维度计算一个预条件子，但是不管是计算还是存储，百万次的百万维度矩阵都几乎是不可处理的。因此从算法上，我们首先就要设计一种新方法来解决这类问题。

2. 计算上的挑战

Shampoo 的权重更新式大概是如下这样的，其中 L 和 R 都是矩阵，它们需要求逆与求根，在计算上会显得非常复杂，这也会拖慢整个迭代的速度。

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量

之前矩阵求逆与根是可以使用 SVD 计算的，但是它们太慢了。因此可以考虑如 Schur-Newton 等一些算法，可以将逆 P 次根问题转换为一系列矩阵-向量和矩阵-矩阵的积，所以对于优化很有帮助。

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量
图 1：在不同维度上，计算某矩阵逆 P 次根的基准对比。Schur-Newton 迭代方法能够在 CPU 上高效运行，而且相比 SVD 有很大的冗余用于提升。

3. 基础设施挑战

神经网络加速器通常是定制的，用来让机器学习程序运行地更快，开销更少。加速器设计倾向于低精度（8bit/16bit），能够满足现有的基准。研究者的方法需要双精度运算，因此已有的加速器甚至都不会启动。

此外，TensorFlow 等深度学习库提供的最优化器 API 适应于随机、一阶梯度下降那种模式。而二阶优化器需要与训练循环做交互，因此从实现上需要对框架底层做出修正。

虽然难，但还是能攻破

三大挑战使实现二阶梯度优化器异常复杂，研究者针对不同的问题提出了一系列优化组件、优化算法。最终搞定的分布式 Shampoo 在 CPU、TPU、GPU 等硬件上高效运行，这也是我们第一次看到二阶优化器在大模型上能 Work 的新研究。

研究者们首先分析了标准的数据并行方法。每个加速器的核都会在一个分批数据上进行前向和反向传播。然后算法会对数据批进行梯度聚合，并使用 all-reduction 的方法获得平均梯度。聚合的梯度被用来进行权重更新。前向和反向传播在所有核中并行计算。

为什么使用 All-reduction？这增加了一个屏障，使得所有核同步聚合批的梯度，并进行权重更新。图 3 中，研究者评价了 Transformer 模型每一步的计算开销。

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量
图 3：使用 Diagonal AdaGrad 优化器的 Transformer 模型的每迭代步延迟时间为 134 毫秒，其中（1）前向传播 57 毫秒；后向传播 71 毫秒；all reduction：4 毫秒；权重更新：2 毫秒。

本文分布式系统实现的整体设计如下图 4 的时间轴所示，具体分布式架构可查阅原论文。

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量
图 4：本文优化算法设计的时间轴。在每一步上计算所有张量的预调节器统计数据。预调节器只在每 N 步上计算，并且计算会分配给训练系统上可用的所有 CPU 核心。运算进行流水线处理，这样就实现了开销均摊。

可实战的二阶梯度优化

研究者在包含 3630 万个句对的 WMT'14 英法标准机器翻译数据集上验证了分布式系统实现方法的有效性。此外，他们在实验中使用了当前 SOTA Transformer 架构，该架构包含 9330 万个参数和 6 层的编码器-解码器结构。

实验在 32 核谷歌 Cloud TPU v3 Pod 上运行，结果如下图 6 所示，本文提出的 Shampoo 算法只需一半迭代数就能实现与 AdaGrad 和 Adam 相同的准确度。

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量
图 6：WMT'14 英法翻译数据集上的 Transformer 模型，Shampoo 二阶梯度算法的收敛速度在迭代数上快了 1.95 倍，且就算要计算二阶梯度，每一次迭代也只慢了 16%，总体上来说节省了 40% 的执行时间。

研究者还利用一个大型 Transformer 模型进行实验，该模型包含 3.754 亿个参数和 6 层的编码器-解码器结构。实验结果如下图 12 所示，端到端的执行时间实现了提升。

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量
图 12：WMT'14 英法翻译数据集上的 Transformer-Big 模型，Shampoo 二阶梯度算法的收敛速度在迭代数上快了 2 倍，且就算要计算二阶梯度，每一次迭代也只慢了 40%，总体上来说节省了 30% 的执行时间。

最后，研究者在 ImageNet-2012 数据集上训练了 ResNet-50 模型，并对使用 SGD+Momentum 的 SOTA 基准方法、本文提出的 Shampoo 二阶梯度算法以及 Adagrad 方法的测试结果进行对比，结果如下图 14 和表 2 所示。

研究者发现，Shampoo 二阶梯度算法虽然未能在测试损失或准确度方面实现任何改进，但与调整好的 SGD+Momentum 基准方法相比，该方法能够更快地减少训练损失。

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量
图 14：在 ImageNet-2012 数据集上训练 ResNet-50 模型时的训练（图左）和测试（图右）交叉熵变化图。

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量
表 2：当训练 ResNet-50 模型的 batch size=4096 时，三种方法在 ImageNet-2012 数据集上的准确度测试结果对比。

相信很多读者都学过最优化方法这类理论课程，我们会发现梯度下降，或者称之为最速下降法是最简单的方法，「锯齿」现象令它在很多领域上都存在问题。我们也会发现各种二阶优化、拟二阶优化在理论上性质远远超过它。然而在深度学习领域，由于数据与模型的规模，我们采用的都是「最速下降法」这个大家庭。

很多时候，我们会想，之前累积的那么多优秀方法，完全应用不到深度学习吗？而这篇论文至少告诉我们，计算、内存等各种困难，我们都是有机会克服的，相信那些具有强硬理论支持的最优化方法，最终会在深度学习展现它们的魅力。
<pre style="max-width: 100%;letter-spacing: 0.544px;text-align: center;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="margin-right: 8px;margin-left: 8px;max-width: 100%;white-space: normal;color: rgb(0, 0, 0);font-family: -apple-system-font, system-ui, "Helvetica Neue", "PingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.544px;widows: 1;line-height: 1.75em;box-sizing: border-box !important;overflow-wrap: break-word !important;"><br  /></section><section style="margin-right: 8px;margin-left: 8px;max-width: 100%;white-space: normal;color: rgb(0, 0, 0);font-family: -apple-system-font, system-ui, "Helvetica Neue", "PingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.544px;widows: 1;line-height: 1.75em;box-sizing: border-box !important;overflow-wrap: break-word !important;"><strong style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;letter-spacing: 0.5px;font-size: 14px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><strong style="max-width: 100%;font-size: 16px;letter-spacing: 0.544px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;letter-spacing: 0.5px;box-sizing: border-box !important;overflow-wrap: break-word !important;">—</span></strong>完<strong style="max-width: 100%;font-size: 16px;letter-spacing: 0.544px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;letter-spacing: 0.5px;font-size: 14px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><strong style="max-width: 100%;font-size: 16px;letter-spacing: 0.544px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;letter-spacing: 0.5px;box-sizing: border-box !important;overflow-wrap: break-word !important;">—</span></strong></span></strong></span></strong></section><section style="max-width: 100%;white-space: normal;font-family: -apple-system-font, system-ui, "Helvetica Neue", "PingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.544px;widows: 1;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section powered-by="xiumi.us" style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="margin-top: 15px;margin-bottom: 25px;max-width: 100%;opacity: 0.8;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="max-width: 100%;letter-spacing: 0.544px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section powered-by="xiumi.us" style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="margin-top: 15px;margin-bottom: 25px;max-width: 100%;opacity: 0.8;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="margin-right: 8px;margin-bottom: 15px;margin-left: 8px;padding-right: 0em;padding-left: 0em;max-width: 100%;color: rgb(127, 127, 127);font-size: 12px;font-family: sans-serif;line-height: 25.5938px;letter-spacing: 3px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;color: rgb(0, 0, 0);box-sizing: border-box !important;overflow-wrap: break-word !important;"><strong style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;font-size: 16px;font-family: 微软雅黑;caret-color: red;box-sizing: border-box !important;overflow-wrap: break-word !important;">为您推荐</span></strong></span></section><p style="margin-right: 8px;margin-bottom: 5px;margin-left: 8px;padding-right: 0em;padding-left: 0em;max-width: 100%;min-height: 1em;color: rgb(127, 127, 127);font-size: 12px;font-family: sans-serif;line-height: 1.75em;letter-spacing: 0px;box-sizing: border-box !important;overflow-wrap: break-word !important;">一文通俗了解对抗生成网络(GAN)核心思想<br style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"  /></p><section style="margin-bottom: 5px;max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;font-size: 14px;box-sizing: border-box !important;overflow-wrap: break-word !important;">MIT最新深度学习入门课，安排起来！</span><br style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"  /></section><p style="margin-right: 8px;margin-bottom: 5px;margin-left: 8px;padding-right: 0em;padding-left: 0em;max-width: 100%;min-height: 1em;color: rgb(127, 127, 127);font-size: 12px;font-family: sans-serif;line-height: 1.75em;letter-spacing: 0px;box-sizing: border-box !important;overflow-wrap: break-word !important;">图深度学习入门难？这篇教程帮你理清楚了脉络<br style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"  /></p><p style="margin-right: 8px;margin-bottom: 5px;margin-left: 8px;padding-right: 0em;padding-left: 0em;max-width: 100%;min-height: 1em;font-family: sans-serif;line-height: 1.75em;letter-spacing: 0px;box-sizing: border-box !important;overflow-wrap: break-word !important;">2020年最值得学习的9大数据分析在线免费课程<br style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"  /></p><p style="margin-right: 8px;margin-bottom: 5px;margin-left: 8px;padding-right: 0em;padding-left: 0em;max-width: 100%;min-height: 1em;color: rgb(127, 127, 127);font-size: 12px;font-family: sans-serif;line-height: 1.75em;letter-spacing: 0px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;-webkit-tap-highlight-color: rgba(0, 0, 0, 0);cursor: pointer;font-size: 14px;box-sizing: border-box !important;overflow-wrap: break-word !important;">深度学习必懂的13种概率分布</span></p></section></section></section></section></section></section></section></section>

二阶梯度优化新崛起，超越 Adam，Transformer 只需一半迭代量

本篇文章来源于: 深度学习这件小事

本文为原创文章，版权归所有，欢迎分享本文，转载请保留出处！

知行编程网
知行编程网 关注：1    粉丝：1
这个人很懒，什么都没写

你可能也喜欢

热评文章

上一篇
下一篇

发表评论

表情 格式 链接 私密 签到
扫一扫二维码分享
 繁