前言
图卷积网络Graph Convolutional Network,简称GCN,最近两年大热,取得不少进展。
最近,清华大学孙茂松教授组在 arXiv 发布了论文 Graph Neural Networks: A Review of Methods and Applications ,作者对现有的 GNN 模型做了详尽且全面的综述。GCN就是GNN中的一种重要的分支。
但是对于GCN的萌新,看着这篇综述可能还是会困难重重、不知所措。
写这篇文章的目的,就是帮助萌新们掌握GCN的重要概念和理论,走出新手村。
什么是Convolution
Convolution的数学定义是:
一般称g为作用在f上的filter或kernel
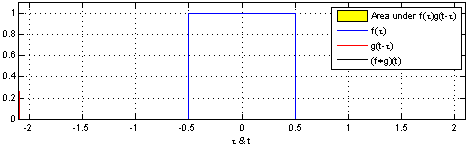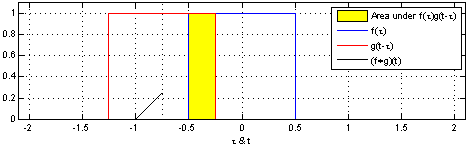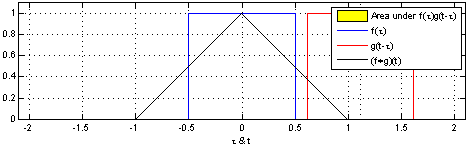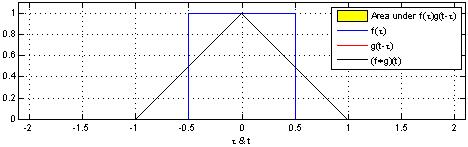
一维的卷积示意图如下:
大家常见的CNN二维卷积示意图如下:
在图像里面卷积的概念很直接,因为像素点的排列顺序有明确的上下左右的位置关系。
那在抽象的graph里面卷积该怎么做呢?
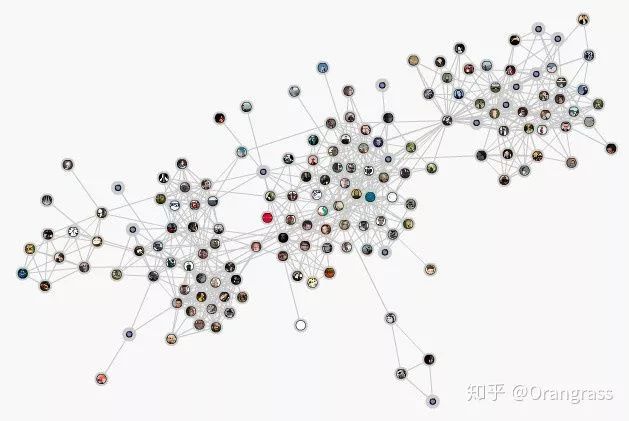
比如这个社交网络抽象出来的graph里面,有的社交vip会关联上万的节点,这些节点没有空间上的位置关系,也就没办法通过上面给出的传统卷积公式进行计算。
Fourier变换
为了解决graph上卷积计算的问题,我们给出第二个装备--Fourier变换。
先上结论,根据卷积定理,卷积公式还可以写成:
这样我们只需要定义graph上的fourier变换,就可以定义出graph上的convolution变换。
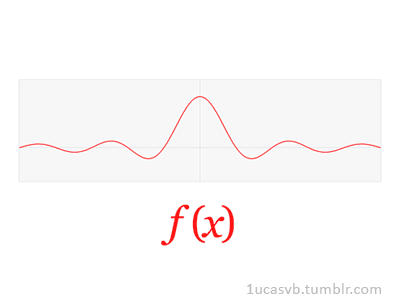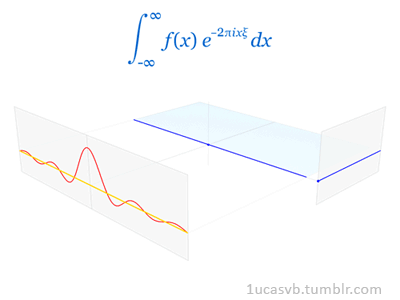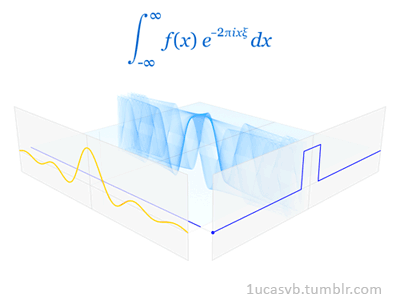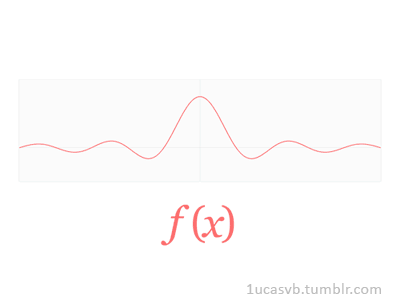
好的,先来看下Fourier变换的定义:
Inverse Fourier变换则是:
根据Fourier变换及其逆变换的定义,下面我们来证明一下卷积定理
我们定义 是 和 的卷积,那么
Laplacian算子
一波未平,又来一个陌生的概念。
不要担心,这是出新手村之前的最后一件装备了。
一阶导数定义为:
laplacian算子简单的来说就是二阶导数:
那在graph上,我们可以定义一阶导数为:
其中y是x的邻居节点
那么对应的Laplacian算子可以定义为:
定义 是 的度数矩阵(degree matrix)
定义 为 邻接矩阵(adjacency matrix)
那么图上的Laplacian算子可以写成
标准化之后得到
定义Laplacian算子的目的是为了找到Fourier变换的基
比如传统Fourier变换的基 就是Laplacian算法的一组特征向量
, 是一个常数
那么图上的Fourier基就是 矩阵的n个特征向量 , 可以分解为
其中 是特征值组成的对角矩阵
那么Graph Fourier变换可以定义为
其中 可以看做是作用在第 个点上的signal,用向量
来表示
是的对偶向量, 是矩阵 的第 行, 是矩阵 的第 行。
那么我们可以用矩阵形式来表示Graph Fourier变换
类似的Inverse Graph Fourier变换定义为
它的矩阵形式表达为
推导Graph Convolution
走到这里,我们已经获得了新手村的所有装备,下面就开始推导GCN的公式。还记得我们之前提到的先上卷积定理吗?
那么图的卷积公式可以表示为:
作为图卷积的filter函数 ,我们希望具有很好的局部性。就像CNN模型里的filter一样,只影响到一个像素附近的像素。那么我们可以把 定义成一个laplacian矩阵的函数
作用一次laplacian矩阵相当于在图上传播了一次邻居节点。进一步我们可以把 看做是 一个laplacian特征值的函数。
改写上面的图卷积公式,我们就可以得到论文SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS(链接:https://arxiv.org/pdf/1609.02907.pdf)的公式(3)
可以看到这个卷积计算的复杂度是非常高的,涉及到求laplacian矩阵的特征向量,和大量的矩阵计算。下面我们考虑对filter函数做近似,目标是省去特征向量的求解
其中 是Chebyshev多项式。这里可以把简单 简单看成是 的多项式。
因为
所以上面filter函数可以写成 的函数
令 ,
那么再加上激活层,我们就可以得到最终的GCN公式:
<pre style="max-width: 100%;letter-spacing: 0.544px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="margin-right: 8px;margin-left: 8px;max-width: 100%;white-space: normal;color: rgb(0, 0, 0);font-family: -apple-system-font, system-ui, "Helvetica Neue", "PingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.544px;widows: 1;line-height: 1.75em;box-sizing: border-box !important;overflow-wrap: break-word !important;"><br /></section><section style="margin-right: 8px;margin-left: 8px;max-width: 100%;white-space: normal;color: rgb(0, 0, 0);font-family: -apple-system-font, system-ui, "Helvetica Neue", "PingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.544px;widows: 1;line-height: 1.75em;box-sizing: border-box !important;overflow-wrap: break-word !important;"><strong style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;letter-spacing: 0.5px;font-size: 14px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><strong style="max-width: 100%;font-size: 16px;letter-spacing: 0.544px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;letter-spacing: 0.5px;box-sizing: border-box !important;overflow-wrap: break-word !important;">—</span></strong>完<strong style="max-width: 100%;font-size: 16px;letter-spacing: 0.544px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;letter-spacing: 0.5px;font-size: 14px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><strong style="max-width: 100%;font-size: 16px;letter-spacing: 0.544px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;letter-spacing: 0.5px;box-sizing: border-box !important;overflow-wrap: break-word !important;">—</span></strong></span></strong></span></strong></section><section style="max-width: 100%;white-space: normal;font-family: -apple-system-font, system-ui, "Helvetica Neue", "PingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.544px;widows: 1;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section powered-by="xiumi.us" style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="margin-top: 15px;margin-bottom: 25px;max-width: 100%;opacity: 0.8;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="max-width: 100%;letter-spacing: 0.544px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section powered-by="xiumi.us" style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="margin-top: 15px;margin-bottom: 25px;max-width: 100%;opacity: 0.8;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><section style="margin-right: 8px;margin-bottom: 15px;margin-left: 8px;padding-right: 0em;padding-left: 0em;max-width: 100%;color: rgb(127, 127, 127);font-size: 12px;font-family: sans-serif;line-height: 25.5938px;letter-spacing: 3px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;color: rgb(0, 0, 0);box-sizing: border-box !important;overflow-wrap: break-word !important;"><strong style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;font-size: 16px;font-family: 微软雅黑;caret-color: red;box-sizing: border-box !important;overflow-wrap: break-word !important;">为您推荐</span></strong></span></section><p style="margin-right: 8px;margin-bottom: 5px;margin-left: 8px;padding-right: 0em;padding-left: 0em;max-width: 100%;min-height: 1em;color: rgb(127, 127, 127);font-size: 12px;font-family: sans-serif;line-height: 1.75em;letter-spacing: 0px;box-sizing: border-box !important;overflow-wrap: break-word !important;">一文通俗了解对抗生成网络(GAN)核心思想<br style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;" /></p><p style="margin-right: 8px;margin-bottom: 5px;margin-left: 8px;padding-right: 0em;padding-left: 0em;max-width: 100%;min-height: 1em;color: rgb(127, 127, 127);font-size: 12px;font-family: sans-serif;line-height: 1.75em;letter-spacing: 0px;box-sizing: border-box !important;overflow-wrap: break-word !important;">关于KN95口罩:可以使用多久?怎么佩戴?<br style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;" /></p><p style="margin-right: 8px;margin-bottom: 5px;margin-left: 8px;padding-right: 0em;padding-left: 0em;max-width: 100%;min-height: 1em;color: rgb(127, 127, 127);font-size: 12px;font-family: sans-serif;line-height: 1.75em;letter-spacing: 0px;box-sizing: border-box !important;overflow-wrap: break-word !important;">IBM Watson大裁70% 员工,撕掉了国内大批伪AI企业最后一块遮羞布!<br style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;" /></p><p style="margin-right: 8px;margin-bottom: 5px;margin-left: 8px;padding-right: 0em;padding-left: 0em;max-width: 100%;min-height: 1em;font-family: sans-serif;line-height: 1.75em;letter-spacing: 0px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="font-size: 14px;">我为什么鼓励你读计算机领域的博士?</span><br style="max-width: 100%;box-sizing: border-box !important;overflow-wrap: break-word !important;" /></p><p style="margin-right: 8px;margin-bottom: 5px;margin-left: 8px;padding-right: 0em;padding-left: 0em;max-width: 100%;min-height: 1em;color: rgb(127, 127, 127);font-size: 12px;font-family: sans-serif;line-height: 1.75em;letter-spacing: 0px;box-sizing: border-box !important;overflow-wrap: break-word !important;"><span style="max-width: 100%;-webkit-tap-highlight-color: rgba(0, 0, 0, 0);cursor: pointer;font-size: 14px;box-sizing: border-box !important;overflow-wrap: break-word !important;">深度学习必懂的13种概率分布</span></p></section></section></section></section></section></section></section></section>
本篇文章来源于: 深度学习这件小事
本文为原创文章,版权归知行编程网所有,欢迎分享本文,转载请保留出处!





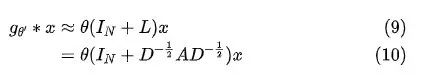


内容反馈