
来源:机器之心
反向传播是深度学习算法中必不可少的组成部分,但是其固有的梯度爆炸(消失),计算速度慢等问题一直困扰着学界。近日,新西兰维多利亚惠灵顿大学的研究者提出了一种新型的算法,可以让深度学习在不依赖反向传播的情况下进行收敛,彻底解决了梯度爆炸问题。同时,研究者表示,只需要额外训练单层的网络就可以达到图像分类中的 SOTA 性能。
论文地址:https://arxiv.org/pdf/1908.01580v1.pdf
-
并行计算各层梯度并更新参数
-
解决梯度消失/爆炸问题
-
降低内存占用
这就是代替反向传播的 HSIC Bottleneck,反向传播传递的梯度它也能计算,反向传播带来的各种缺点它也能弥补。
在这篇论文中,研究者介绍了用于训练深度神经网络的希尔伯特·施密特独立准则(Hilbert-Schmidt independence criterion,HSIC)Bottleneck,用它来代替反向传播简直非常美妙了。
研究者表示,HSIC-Bottleneck 的表现在 MNIST/FashionMNIST/CIFAR10 分类中的表现与具有交叉熵目标函数的反向传播算法相当。且只需要在训练好的、已冻结参数 HSIC-Bottleneck 网络上再增加一个基于 SGD 且没有反向传播一层网络能够实现图像分类的 SOTA 性能。

虽然很多研究者都知道我们应该找一种比反向传播更优秀的方法,但反向传播应用太广了,也非常直观优美。因此,很难有研究者提出真正能 Work,且还非常有优势的 BP 替代品。在这篇论文放到 Reddit 后,很多研究者都非常赞同这项工作,并表示这个领域非常值得关注。
DontShowYourBack 表示:「这篇论文的附加值并不在于它是否达到了 SOTA 结果,在我看来,作者设法使用了一种既不复杂、又不需要对称反馈的机制,并获得了很好的效果,这才是真正重要的因素。理论上,它能应用于更低计算力的平台和更独特的架构,因为这些是将反向传播应用到当前硬件和架构上最大的挑战。
该用户表明,他将亲自研究这种方法,并希望能快速看到一些有趣的结果。
HSIC Bottleneck 的作者表示,反向传播计算梯度的复杂度为 O(D^3),其中 D 表示不同层级的神经元数量。因此整个神经网络的反传复杂度为 O(LD^3),其中 L 表示层级数。但是对于 HSIC 来说,它的计算复杂度为 O(M^2),其中 M 表示样本数量,这样整个网络的计算复杂度为 O(LM^2)。
值得注意的是,目前深度模型都是过参数化的,也就是说参数量要远远多于数据量,这样计算量不就大大降低了吗?
因此有用户表明:「HSIC 最重要的部分就是将复杂度由反向传播的 O(D^3) 降低到 O(M^2),这对于拥有数百万或数十亿参数量的神经网络来说极其重要。」
HSIC 还有很多受到关注的属性,目前机器学习社区也都在讨论它。
既然神经网络可以视为一个复杂的复合函数,且复合的次数就等于层级数,那么将复合函数的求导法则「链式法则」作为导数的获取方式就非常直观了。但最直观的方法并不一定是最优的方法,反向传播经常会因为各种缺陷刺激着一批批研究者探索新的方法。
尽管反向传播非常实用、优美,但它的速度、内存占用、梯度消失/爆炸问题都困惑着一代代研究者。因为前面层级的梯度必须等后面层级的梯度算完,BP 的速度比较慢;因为 BP 需要保存前向传播的激活值,所以显存占用比较高;因为链式传播的连乘方式,梯度非常容易爆炸或消失。
这些都是急需解决的问题,连提出 BP 的 Geoffrey Hinton 都对它充满了质疑,在 17 年的 CapsNet 中,Hinton 老爷子尝试通过 Dynamic Routing 找到更好的解,而且这种迭代并不需要反向传播。Hinton 很早就意识到反向传播并不是自然界生物大脑中存在的机制,也希望找到更好的反馈机制。
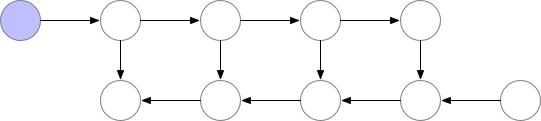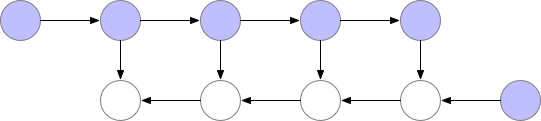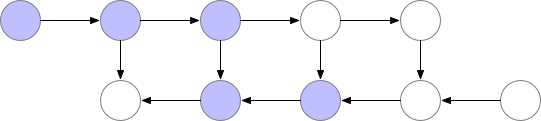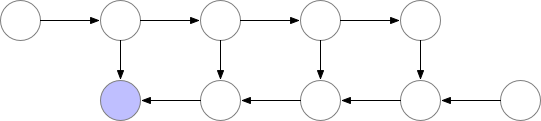
标准前传与反传的计算流程,其中紫色点表示计算结果需要保存在内存中。
针对传播速度,DeepMind 之前曾提出了一种名为解耦层的方法,它采用合成梯度近似经 BP 传播的梯度,从而使前面层级与后面层级一同更新。而针对内存占用,OpenAI 也曾尝试做一个算力与内存间的权衡,他会以某种方式重算部分前传结果,从而降低内存占用。
但只要反传还是链式法则,梯度消失和爆炸就不会真正得到解决。在这篇最新的论文中,研究者表示,如果我们直接最大会隐藏层与标注间的互信息,最小化隐藏层与输入的相互依赖性,我们我们就能直接获得对应的梯度,这种梯度是不需要反向传播进行分配额的。因此模型在不要那么多内存下快速更新权重参数,同时这样也不会出现梯度爆炸或消失问题。
在论文中,研究人员说明,即使没有反向传播,模型依然可以学习分类任务,并获得相当有竞争力的准确率。他们因此提出了一种深度学习网络训练方法。
这一方法由使用近似信息瓶颈的方法训练而来。只要最大化隐层表示和标签之间的互信息,并在同时最小化隐层表示和输入的互相依赖关系即可。从信息瓶颈的角度来说,为了减少模型依赖的参数量,所以要尽可能的让隐层表示减少从输入数据中获得的信息量,而要尽可能让隐层最大化地「榨干」学习到的隐层表示,输出正确的标签预测结果。因此这一过程可以在尽可能减少数据依赖的情况下获得能够预测结果的信息。
由于计算互信息在随机变量中较为困难,研究人员选择了基于非参数核的方法——希尔伯特·施密特独立准则(HSIC),用来刻画不同层之间的统计学依赖。换句话说,对于每个网络层,研究人员都会同时最大化层和期望输入之间的 HSIC,并最小化层和输入之间的 HSIC。
研究人员进一步证明,按照这样的训练方式,网络中的隐层单元可以组成很有用的表示。具体来说,冻结训练好的 HSIC 网络,在不需要反向传播的情况下,仅更新和训练一层单层的、使用了卷积 SGD 的网络就可以达到很近似最佳准确率效果的模型
使用 HSIC-Bottleneck 的优势在于,相比标准的反向传播算法,网络可以快速收敛。这是因为 HSIC-Bottleneck 直接在连续随机变量上进行运算,相比基于丢弃的传统信息瓶颈方法更好。这一方法使用了一个传统的弱训练网络用于将表示转换为输出标签的形式。在实际中,研究人员使用了一个网络,包括很多层和多种维度(如果是全连接层),或者不同数量的核(如果是卷积层)作为开始。
说起希尔伯特·施密特独立准则,我们需要先谈谈信息瓶颈的问题。信息瓶颈描述的是最小需要多少数据能够充分预测结果的理论,这是一个隐层表示上的权衡问题,即可以预测输出所需的信息量和输入中应当保留多少信息之间的权衡。信息瓶颈原则决定了需要保留多少关于标签的隐层表示信息,而需要压缩多少输入中的信息。
根据信息瓶颈,我们就可以知道,在训练机器学习模型时,需要对至少多少的输入信息进行保留,以便隐层表示能够预测出和标签相符结果的数据量。
而要计算这个保留的信息量是非常困难的。此外,传统的信息瓶颈理论大部分基于丢弃信息的方法,因此作者选择了基于希尔伯特·施密特独立准则的信息瓶颈方法,用于获得机器学习过程中的梯度。
那么,什么是希尔伯特·施密特独立准则呢?理论上,希尔伯特·施密特独立准则可以发现变量之间的任意依赖。当给定正确的核大小(如高斯核)的时候,HSIC 当且仅当两个随机变量完全独立时为 0。因此,只要是两个变量之间具有非独立的关系,HSIC 就可以以非参数化的方式将其刻画出来。
使用 HSIC-Bottleneck 目标训练深度学习的网络被称为 HSIC-Bottleneck 训练或预训练。Bottleneck 训练网络的输出包括分类的必要信息,但不是正确的形式。
研究人员评价了两种从 HSIC 评价训练网络产生分类结果的方法。首先,如果输出是独热向量,则可以根据训练标签被直接重新排列。在第二个场景下,研究人员将一个单层和 softmax 输出层连接到了冻结的 Bottleneck 训练网络后,并使用没有反向传播的 SGD 方法训练这个额外增加的层。这一步骤被称为后训练(post-training)。
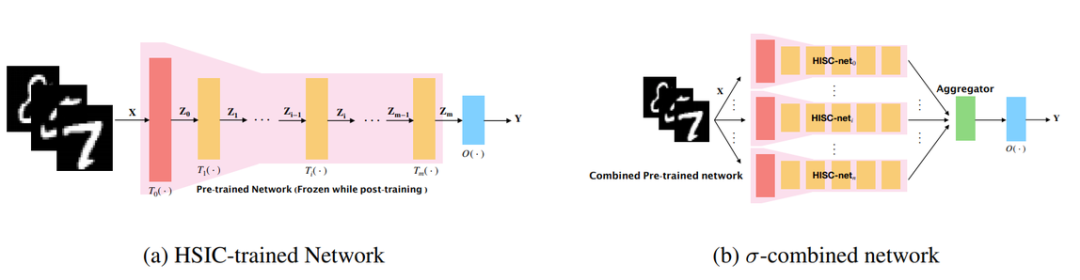
图 1:HSIC 训练的网络(1a)。这是一个标准的前向传播网络,但是使用了 HSIC IB 目标函数,这样可以使最后一层的隐层表示快速地开始训练。图 1b 则展示了一个名为「σ-组合」的网络,每个网络分支都有一个特定的σ进行训练。因此,对于从 HSIC 网络中训练的每个隐层表示都可能包含在特定尺度下从 HSIC-Bottleneck 目标函数中获得的不同信息。之后,聚合器会将隐层表示相加,组成一个输出表示。
研究人员展示的 HSIC 训练网络是如下的一个前向输入网络。
在网路中,Z = {Zi}, i ∈ {0, ..., L},L 则是隐层的数量。HSIC 训练网络可以被理解为是优化的编码 PθT (Zi |X) 层和 PθT (Y |Zi) where i ∈ {0, ..., L} 解码层。这个网络提供了包含用于分类任务信息的隐层。
首先,研究者绘制了 HSIC-bottleneck 值与激活值的分布,它们都是在训练中从简单的模型采样得出。其次,研究者还提供了 HSIC-bottleneck 和标准反向传播之间的对比,它们都在相同数据集上使用相同参数量的前馈网络测试得出。
在对比实验中,研究者在 MNIST/Fashion MNIST/CIFAR-10 数据集上训练前馈网络,并分析了 HSIC-bottleneck 在处理经典分类任务上的表现。其中,前馈网络还包括非常著名的 ResNet。在研究者完成的所有实验中,都包含了标准反向传播、预训练和后训练阶段,后训练阶段使用的都是 SGD 最优化器。
图 2 展示了 HSIC-bottleneck 的值在训练深度网络时的变化。
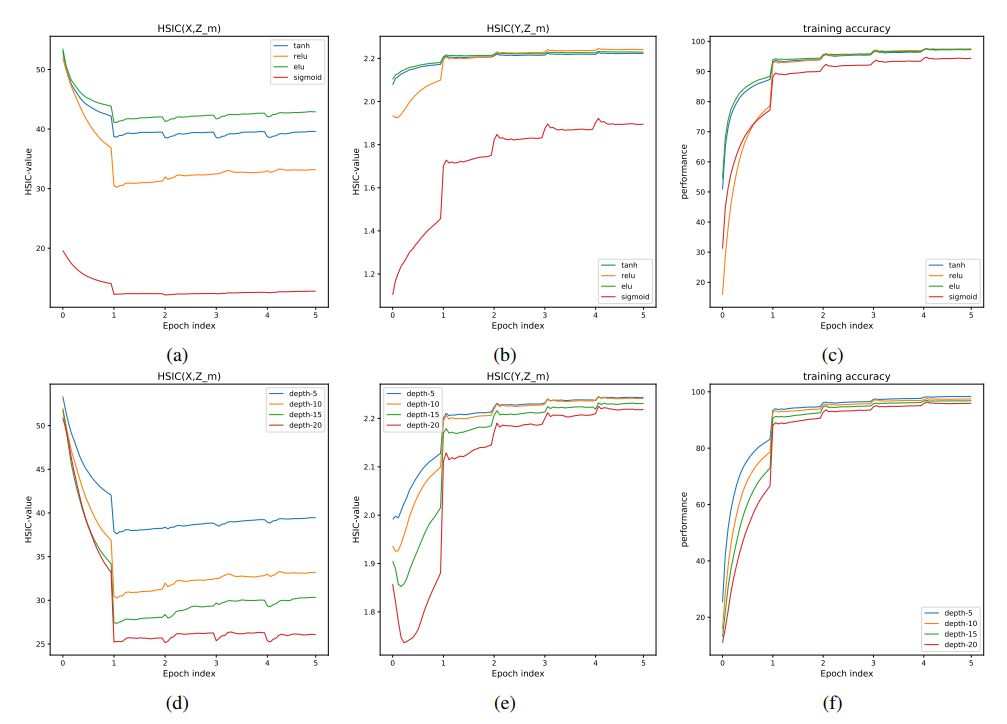
图 2:这些实验展示了,在传统反向传播训练过程中,随着网络激活函数 (2a)-(2c) 和深度 (2d)-(2f) 的变化,HSIC-bottleneck 数量 HSIC(X, ZL) 和 HSIC(Y, ZL) 的变化,以及训练准确率的变化。
图 3a 和 3b 可视化了前馈网络中最后一个隐藏层每一个类别的激活值。
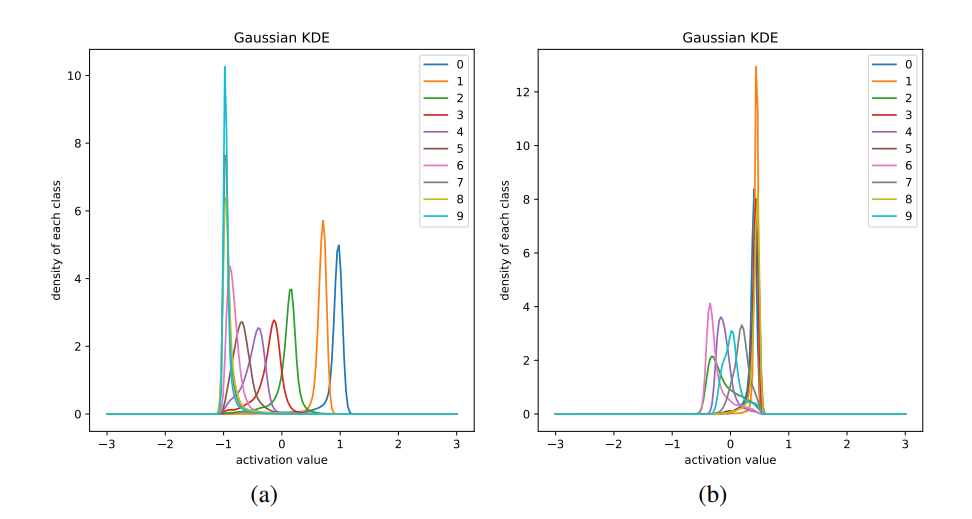
图 3:最优一层 tanh 激活函数值的分布,其神经网络各层的隐藏单元数为:784-64-32-16-8-4-2-1,它通过 HSIC-bottleneck 目标 (3a) 和反向传播 (3b) 训练。
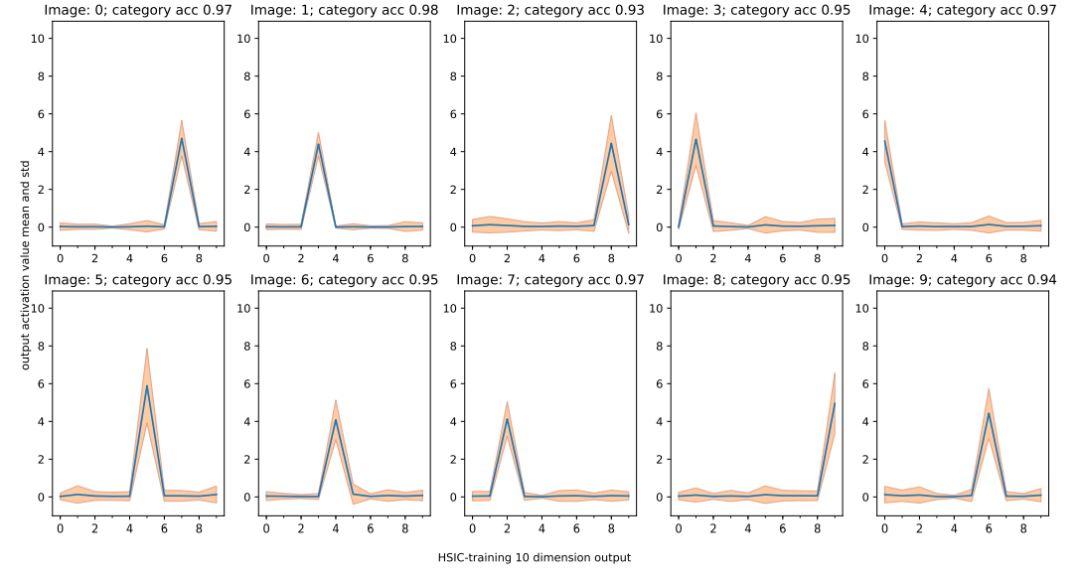
图 4:MNIST 输出类别的分布,每一张子图都展示了类别及对应的分类准确率。
图 5 展示了反向传播和论文提出的 HSIC 评价训练方法。在第一个训练轮中,论文提出的方法的表现就超过了标准的机器学习训练方法,分别在 Cifar 10,FashionMNIST 和 MNIST 上取得了 43%、85% 和 95% 的效果。在训练结束后,HSIC-Bottleneck 训练的网络表现和其他标准反向传播算法几乎一致。
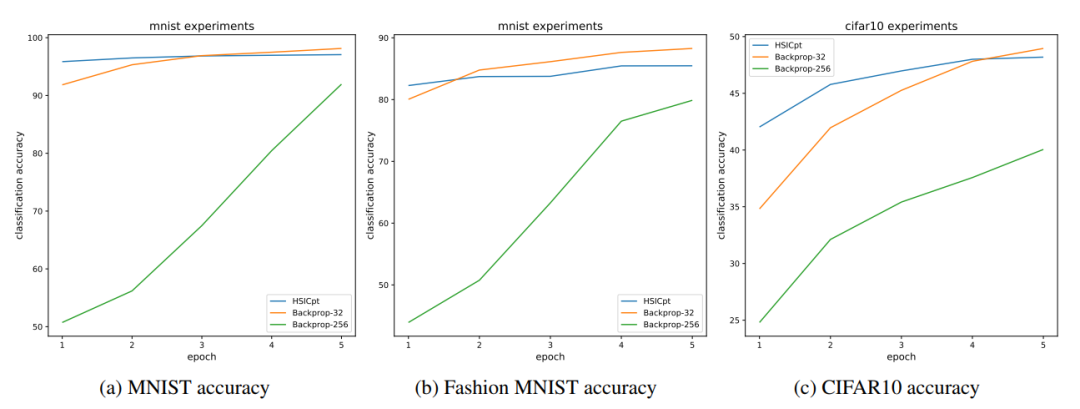
图 5:论文提出的 HSIC 评价训练方法在标准的分类问题上的表现。实验使用了同样的训练配置,但是批大小不同。传统反向传播使用了 32 和 256 的批大小,但 HSIC 算法只使用了 256 的批大小。
在图 8 中,研究人员展示了一个有着 5 个卷积残差块的 HSIC 训练的网络在不同数据集上的表现。每个实验都包括了 50 个 HSIC 训练轮,之后每个网络都会进行后训练——用一个单层分类网络进行,这和标准反向传播训练网络不同。
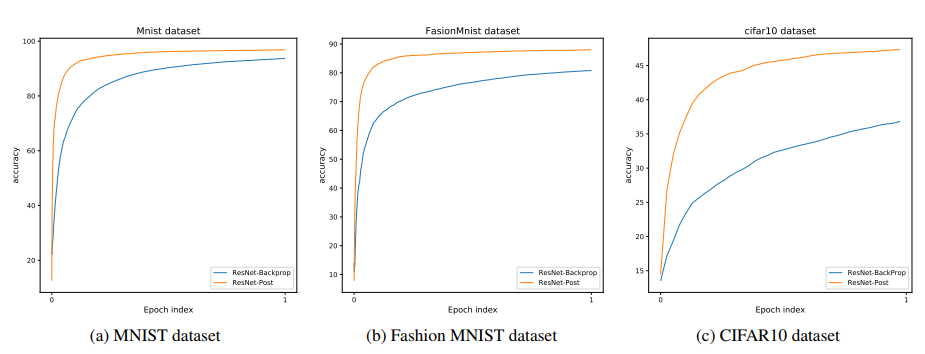
图 8:在不同数据集上 ResNet 后训练的效果。
相关链接:https://arxiv.org/abs/1908.01580v1
https://www.reddit.com/r/MachineLearning/comments/cql2yr/deep_learning_without_backpropagation/
为您推荐
微软 VS Code 已原生支持 Jupyter 笔记本,再也不用打开网页调试运行了
作为 IT 行业的过来人,你有什么话想对后辈说的?
本篇文章来源于: 深度学习这件小事












内容反馈