
一只小狐狸带你解锁 炼丹术&NLP 秘籍
前言
需要许多时间步计算的循环神经网络,如LSTM、GRU,往往存在梯度爆炸的问题。其目标函数可能存在悬崖一样斜率较大的区域,这是由于时间步上几个较大的权重相乘导致的。当参数接近这样的悬崖区域时,如果更新梯度不足够小,很有可能就会直接跳过这样的悬崖结构,然后被弹射到非常远的地方。梯度裁剪(gradient clipping),是这类问题的常用解决办法。它的核心思想就是根据目标函数的光滑程度对梯度进行缩放[1]。
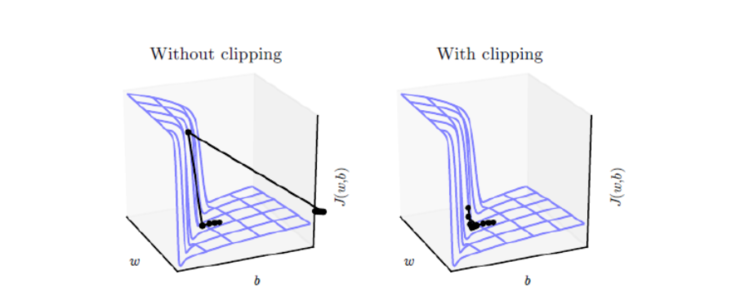
本文介绍来自MIT的一篇ICLR2020满分论文《Why gradient clipping accelerates training: A theoretical justification for adaptivity》。顾名思义,这篇论文就是分析为什么梯度裁剪能加速深度学习的训练过程。原文很长,公式很多,还有不少研究复杂性的概念,说实话对笔者来说里边的大部分内容也是懵的,不过大概能捕捉到它的核心思想:引入了比常用的L约束更宽松的约束条件,从新的条件出发论证了梯度裁剪的必要性。本文就是来简单描述一下这个过程,供读者参考。
论文链接:https://arxiv.org/pdf/1905.11881.pdf
Arxiv访问慢的小伙伴也可以在订阅号后台回复关键词【0615】下载论文PDF。
梯度裁剪
假设需要最小化的函数为,就是优化参数,那么梯度下降的更新公式就是(滑动查看完整公式)
其中就是学习率。而所谓梯度裁剪(gradient clipping),就是根据梯度的模长来对更新量做一个缩放,比如
或者
其中 ,是一个常数。这两种方式都被视为梯度裁剪,总的来说就是控制更新量的模长不超过一个常数。其实从下面的不等式就可以看到其实两者基本是等价的:
L约束
有不少优化器相关的理论结果,在其证明中都假设了待优化函数的梯度满足如下的L约束:
由于 是梯度的波动程度,实际上衡量的就是 的光滑程度,所以上述约束也称为“L光滑性条件(L-smooth)”[2]。值得提醒的是,不同的场景可能会需要不同的L约束,比如有时候我们要假设模型输出关于输入满足L约束,有时候我们要假设模型输出关于参数满足L约束,而上面假设的是模型 loss 的梯度关于参数满足L约束。如果条件 (5) 成立,那么很多优化问题都将大大简化。因为我们可以证明[3]:
对于梯度下降来说,,代入上式得到
因此,为了保证每一步优化都使得 下降,一个充分条件是 ,即 ,而 的最小值在 时取到,所以只需要让学习率为 ,那么每步迭代都可以使得 下降,并且下降速度最快。
放松约束
条件 (5) 还可以带来很多漂亮的结果,然而问题是在很多实际优化问题中条件 (5) 并不成立,比如四次函数 。这就导致了理论与实际的差距。而本文要介绍的论文,则引入了一个新的更宽松的约束:
也就是将常数 换成动态的 ,原文称之为“(L0, L1)-smooth”,这里也称为“(L0, L1)约束”。显然这个条件就宽松多了,比如可以检验 是满足这个条件的,因此基于此条件所推导出的理论结果适用范围会更广。
在新的约束之下,不等式 (6) 依旧是成立的,只不过换成对应的动态项:
代入得到
所以很明显了,现在要保证每一步下降,那么就要求
以及最优学习率是
这就导出了梯度裁剪 (3)。而保证了每一步都下降,那么就意味着在优化过程中每一步都没有做无用功,所以也就加速了训练过程。
作者们是怎么提出这个条件 (8) 的呢?论文中说是做实验观察出来的:观察到损失函数的光滑程度与梯度模长呈“线性相关”关系.png,如下图所示。但笔者感觉吧,至少应该还有些从结果反推的成分在里边,不然谁那么无聊会去观察这两者的关系呢?
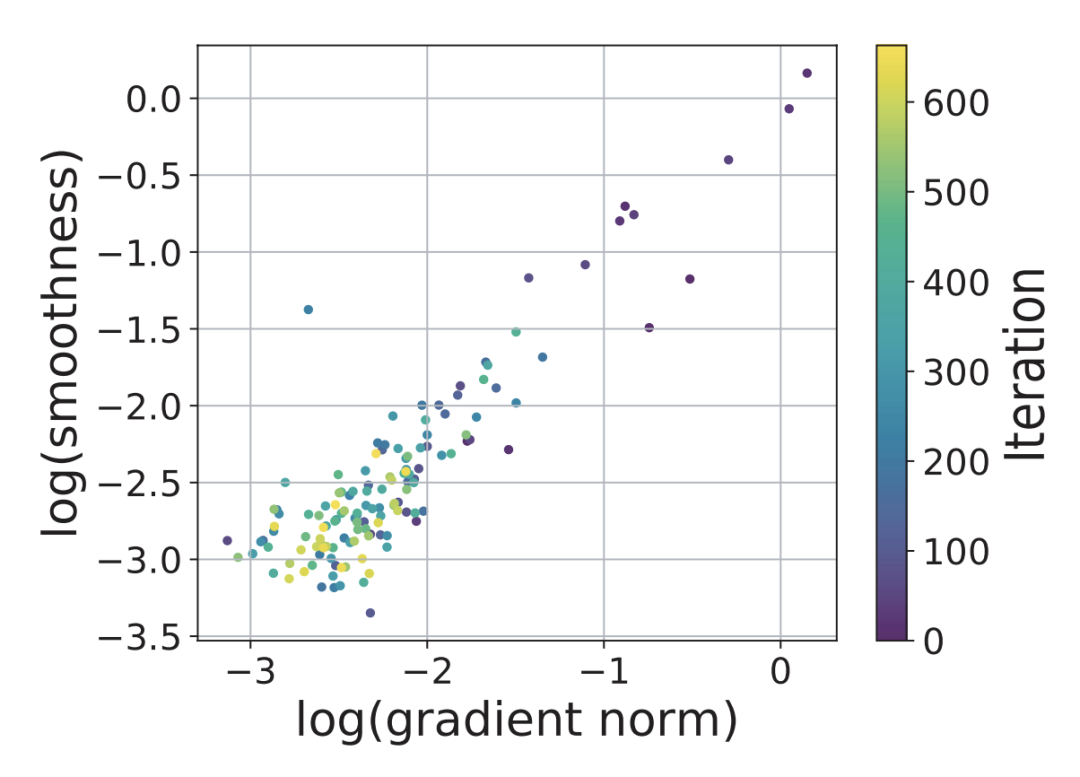
文章小结
本文简要介绍了ICLR2020的一篇分析梯度裁剪的满分论文,主要思路是引入了更宽松普适的假设条件,在新的条件下能体现出了梯度裁剪的必要性,并且由于放松了传统的约束,因此理论结果的适用范围更广,这也就表明,梯度裁剪确实是很多场景下都适用的技巧之一。
参考文献 lan Goodfellow et. al, "Deep Learning", MIT press, 2016
[2]
关于L约束可以作者其他博客: 《深度学习中的Lipschitz约束:泛化与生成模型》、《BN究竟起了什么作用?一个闭门造车的分析》。
[3]
证明过程可参考https://kexue.fm/archives/6992。
本文为原创文章,版权归知行编程网所有,欢迎分享本文,转载请保留出处!




内容反馈