暴力匹配(BF)
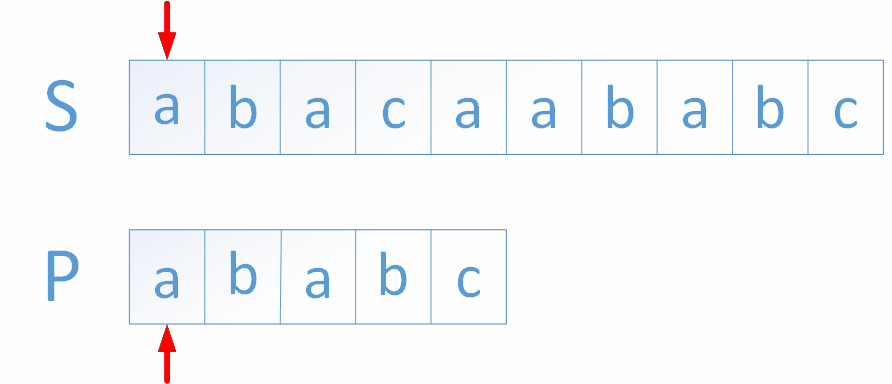
字符串匹配是我们编程中常见的问题。从一个字符串（主字符串）中检测另一个字符串（模式字符串）是一个非常经典的问题。提到这个问题，我们首先想到的可能是算法暴力匹配，下面的动图展示了暴力匹配的过程。
上图中，当箭头所指的字符全为蓝色时，表示两者匹配，全为黑色时，表示两者不匹配，红色表示在main中找到模式串细绳。
该算法的总体思路是，每当模式串和主串出现字符不匹配时，模式串和主串对应的位置整体向后移动一位。
再次从模式串的第一位开始比较，重复上述方法，直到在主串中匹配到模式串或者匹配到主串的最后一位。
如果主串和模式串都比较短，使用暴力匹配还是不错的选择，编码也比较容易；
但是如果主串和模式串太长，我们想想就知道这个过程非常耗时，那么会不会有相应的优化算法呢？
下面介绍一下本文的主角——KMP算法。废话不说，直接说算法的应用过程和使用Python实现算法的代码。最后，通过对两者时间复杂度的分析，总结一下为什么KMP算法会比蛮力匹配算法好。
KMP算法
构建前缀表
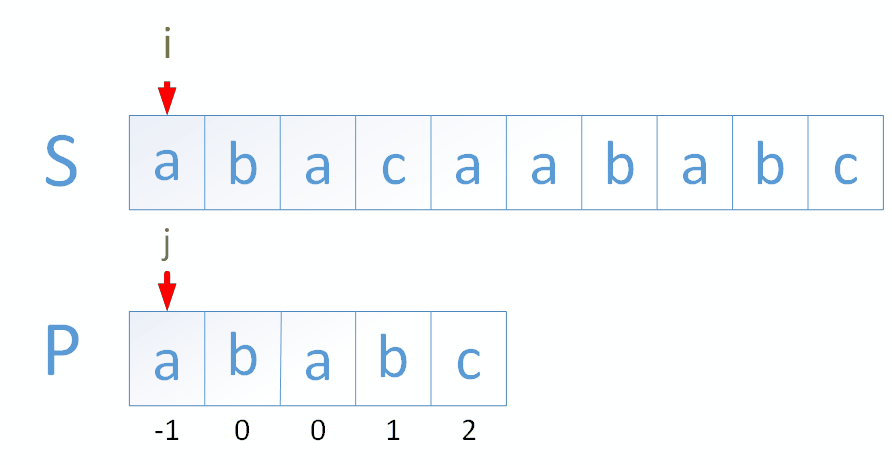
我们首先要确定一下引例的主串和模式串：
主 串 S = “abacaababc”
模式串P=“ababc”
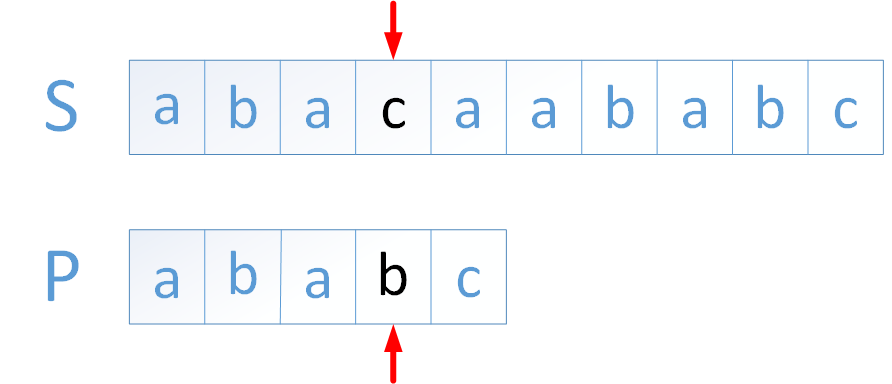
当模式串与主串相匹配时，我们暂时只看第4步。显然，主串S中的c和模式串P中的b不匹配：
如果使用暴力匹配算法，则将模式串P向后移动，从P的第一个字符开始比较。但是现在通过匹配可以知道，当第四位不匹配时，可以肯定的是前三个字符是“aba”。这个已知信息非常有用。
KMP算法的核心是利用匹配失败后得到的信息，尽量减少模式串与主串的匹配次数，从而达到快速匹配的目的。比如对于这种不匹配的现象，我们是不是可以这样直接移动模式串呢？
那么信息从何而来？在KMP算法中，对于一个模式串，可以先计算其内部的匹配信息，这样当匹配失败时，可以最有效地移动模式串，从而减少匹配次数。在此之前，你需要了解前缀和后缀。
前缀：abcde的前缀可以是a、ab、abc、abcd
后缀：abcde的后缀可以是e、de、cde、bcde
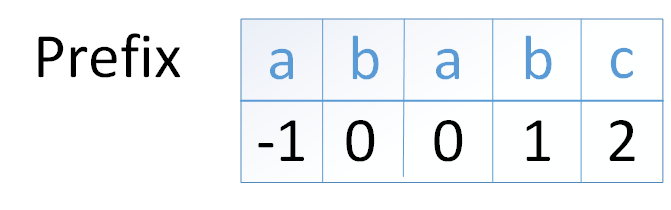
这里需要引入一个新的概念——前缀表，可以用profix表示，下标从0开始。profix[i]存储的信息是前i+1个字符的最长公共前缀和后缀，而最长的公共前缀和后缀的长度必须小于字符串的长度。
可以看到"ababc"不是前后缀，但也被列到了表中。
如果你了解过 KMP 算法，你可能听说过下一个数组。前缀表转换为下一个数组时，会覆盖最后一位的值，对流程没有影响。
由于本文只依赖前缀表profix来完成KMP算法，所以接下来的数组就不多说了。方法不同只是表述不同，归根结底原理还是一样的。
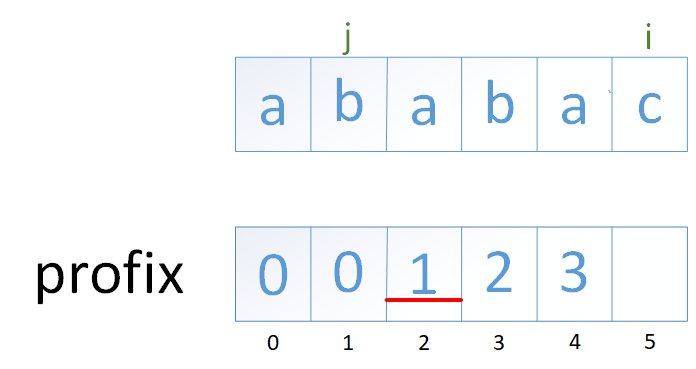
上面的前缀表是通过肉眼对比得到的。程序毕竟不是人，所以需要通过程序可以识别的方法来构造前缀表，按照下图来描述这个过程。
通过这张图，前缀表的构建可以规划为以下五个步骤：
2、首先创建两个指针，指针j指向模式串的第一位（下标为0），指针i指向模式串的第二位（下标为1）。
2、由于模式字符串开头是单个字符，没有前缀和后缀，所以对应的前缀表的第一位永远为0。
3、当j=0时，比较j和i指向的字符。如果字符不匹配，则用0填充i对应的前缀表位置，并向后移动i，j不变。
4、当j和i指向的字符匹配时，将i对应的前缀表位置填入(j+1)，j和i都向后移动一位。
5.如果j和i指向的字符不匹配，且此时j≠0，j需要回到profix[j-1]的位置，
再次与i指向的字符进行比较，重复此步骤，直到j匹配到i指向的字符或j=0。
连着图看完这五个步骤，估计第五步你还看不懂。看懂了，只能感叹牛逼了。使用下面的例子可以更好的突出第五步的回溯机制。
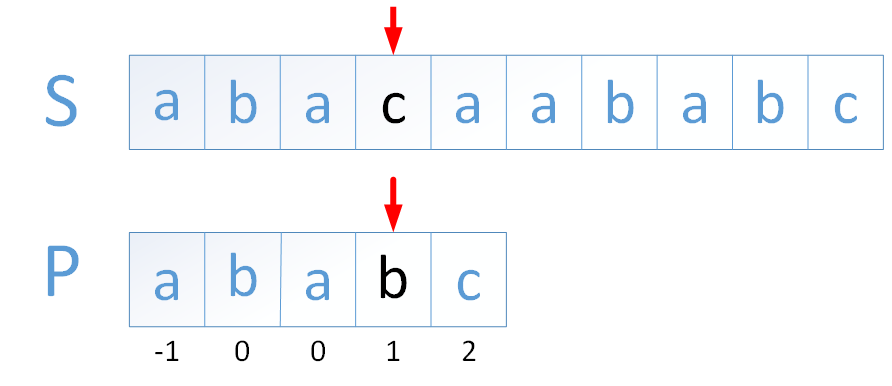
按照上面的步骤，我写出了前缀表的前五位。此时j和i指向的字符不匹配，j≠0。这里j的下标为3，所以我们需要在前缀表中找到下标j-。 1的值，即profix[2]，然后j回溯到对应的位置。
这个回溯是因为匹配j和i之间的字符串的前缀可以在模式串的头部找到，即本例中的a。如果此时j和i指向的字符匹配，那么最长公共前缀后缀的长度就是匹配到的前缀(a)的长度加1。可以看出，如果j和i之间的字符串i 很长，这个操作可以节省很多时间。
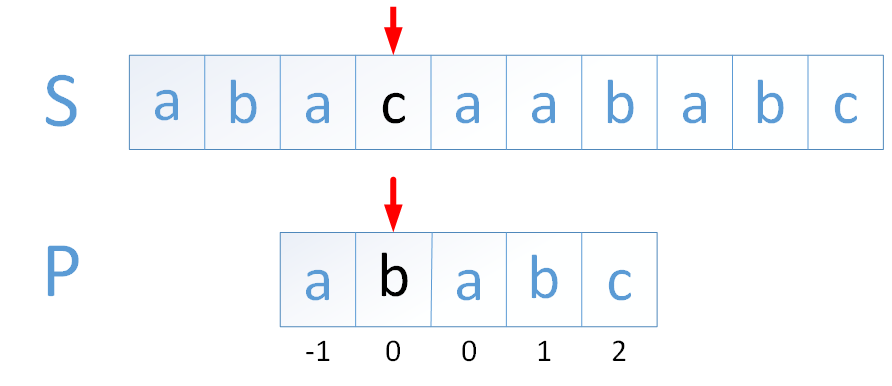
此时j和i指向的字符仍然不匹配，则需要继续回溯j，方法同上，回溯位置为profix[0]。
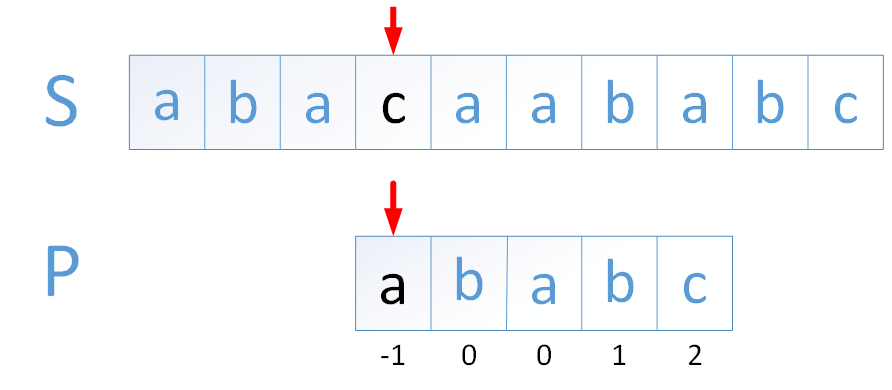
此时j和i指向的字符还是不匹配，但这里需要做的就不是回溯了，因为j=0已经满足回溯结束条件，只需将i对应前缀表的位置(profix[5])中填入0即可，用肉眼匹配也会发现此时的确没有公共前后缀。
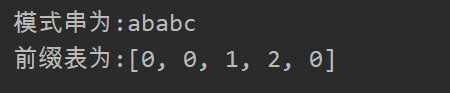
在理解上述步骤之后，可以将其当成伪代码，依据伪代码很容易编写出构建前缀表函数。
def PrefixTable(Pattern):
i = 1;j = 0
prefix = [0]*len(Pattern)
while(i<len(Pattern)):
if Pattern[j]==Pattern[i]:
prefix[i] = j+1
j+=1;i+=1
else:
if j == 0:
prefix[i] = 0
i+=1
else:
j = prefix[j-1]
return prefix你可以输入一个模式字符串来测试代码是否可以得到对应的前缀表。
优化前缀表
经过上面的解释，你可能会发现一个基本的事实，即前缀表的最后一位是没有作用的。这是什么原因？因为当j和i指向的字符不匹配时，这里的解决办法是回溯j，而回溯的依据永远是prefix[j-1]，j永远不能超过i，所以前缀表的最后一位会永远不会被使用。
然后可以去掉最后一位，将所有元素后移一位，前缀表的第一位补-1，如下图：
填写-1的操作原理后面结合图片会更容易理解。目前我们只需要知道这个操作，了解它对应的代码即可。
def MoveTable(prefix):
for i in range(len(prefix)-1,0,-1):
prefix[i] = prefix[i-1]
prefix[0] = -1
return prefix
KMP匹配机制
主串和模式串还是沿用上面的例子，这里省略了一些简单的匹配过程，直接看重点。
可以看出主串的第4位和模式串不匹配，现在要做的是将Pattern[prefix[4]]匹配到主串中需要匹配的元素，即就是，将模式串中下标为1的元素移动到主串第4位对应的位置，从图中可以理解。
对应的位置还是不匹配，需要将模式串向后移动。该位置对应的前缀表的值为0，所以Pattern[prefix[0]]对应主串中需要匹配的元素，即模式串下标为0的元素对应主弦的位置。
这时候两个字符串对应的位置还是不匹配，但是a已经是pattern字符串的第一个元素了。如果需要继续按照上述方法将模式串向后移动，让主串的位置匹配模式串中下标-1的元素，但是前缀表中没有下标-1的元素.
因此，如果比较时模式串与主串对应位置不匹配，且模式串元素对应的前缀表的值为-1，则直接将整个模式串后移一位，并将指向主字符串的指针向后移动一位即可，这就是为什么在前缀表的第一位插入-1 的原因。
下图展示了使用KMP算法在主串中寻找模式串的整个过程。
KMP算法的代码如下：
def KMP(TheString,Pattern):
m = len(TheString);n = len(Pattern)
prefix = PrefixTable(Pattern)
prefix = MoveTable(prefix)
i = 0;j = 0#i为主串指针，j为模式串指针
while(i<m):
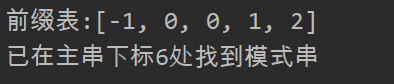
if j==n-1 and TheString[i]==Pattern[j]:
print("已在主串下标%d处找到模式串" % (i-j))
j = prefix[j]
if TheString[i]==Pattern[j]:
i+=1;j+=1
else:
j = prefix[j]
if j==-1:
i+=1;j+=1这里只讲第一个if语句。当j指向模式串的最后一位时，如果此时主串和模式串的对应位置匹配，则说明在主串中找到了模式串，打印出第一个。角色出现的地方。
j=prefix[j]j = prefix[j]j=prefix[j]的作用是找到模式串后继续匹配剩下的主串，因为主串中可能有多个模式串出现。
最后整个程序运行截图如下：
BF与KMP比较
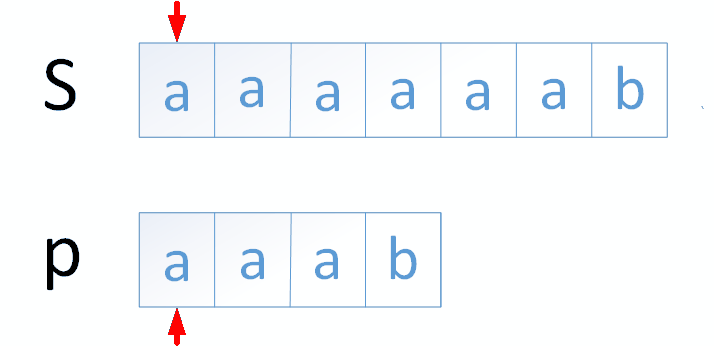
为什么KMP比BF好，这里通过比较两者的时间复杂度来说明原因，假设有两个极端的主串和模式串：
主 串 S = “aaaaaaab”
模式串P=“aaab”
首先看一下BF算法解决该匹配问题的流程：
然后再看一下KMP算法解决该匹配问题的流程：
假设主串长度为m，模式串长度为n。对于BF算法，每当遇到不匹配的字符，都必须从模式串的开头重新匹配，所以对应的时间复杂度为O(m∗n)O(m*n)O(m∗n)；
对于KMP算法，每当遇到不匹配的字符时，不会根据得到的信息重复匹配的已知前缀，所以对应的时间复杂度为O(m+n)O(m+n)O(m+名词）。当字符串较长时，KMP算法在时间复杂度上完全优于BF算法。
总结
我个人认为KMP算法并不难。关于这个算法的博客和视频有很多，但各不相同。虽然原理大致相同，但是不要同时看前缀表和下一个数组。因为这两个很相似，所以会很容易。迷茫，可以先看懂前缀表再看下数组相关的知识点，这样对KMP的理解才算透彻。
本文为原创文章，版权归知行编程网所有，欢迎分享本文，转载请保留出处！
内容反馈