三剑客之Scipy
前面说了,原来的numpy其实是scipy的一部分,后来才从scipy中分离出来的。 scipy函数库在numpy库的基础上增加了很多数学、科学和工程计算中常用的库函数。比如线性代数,常微分方程的数值解,信号处理,图像处理,稀疏矩阵等等。由于涉及的领域比较多,我对scipy就像是瞎子摸大象,摸到的地方只能数数.
一、插值
数据插值是数据处理中经常使用的一种技术。常用的插值有一维插值、二维插值、高阶插值等,常用算法有线性插值、B样条插值、邻近插值等。
1、一维插值
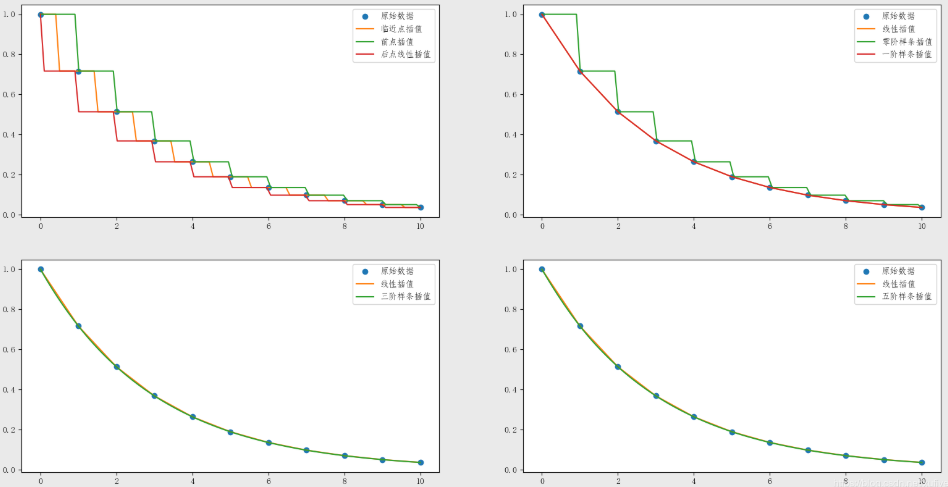
一维插值最常用的算法是线性插值和三阶样条插值。此外还有前点插值、后点插值、邻点插值、零阶插值(相当于前一点插值)、一阶插值(相当于线性插值)、五阶插值等。 以下例子对比了上面8种插值方法。
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['FangSong']
plt.rcParams['axes.unicode_minus'] = False
x = np.linspace(0,10,11)
y = np.exp(-x/3.0)
x_new = np.linspace(0,10,100) # 期望在0-10之间变成100个数据点
f1 = interpolate.interp1d(x, y, kind='linear')
f2 = interpolate.interp1d(x, y, kind='nearest')
f3 = interpolate.interp1d(x, y, kind='zero')
f4 = interpolate.interp1d(x, y, kind='slinear')
f5 = interpolate.interp1d(x, y, kind='cubic')
f6 = interpolate.interp1d(x, y, kind='quadratic')
f7 = interpolate.interp1d(x, y, kind='previous')
f8 = interpolate.interp1d(x, y, kind='next')
plt.figure('Demo', facecolor='#eaeaea')
plt.subplot(221)
plt.plot(x, y, "o", label=u"原始数据")
plt.plot(x_new, f2(x_new), label=u"临近点插值")
plt.plot(x_new, f7(x_new), label=u"前点插值")
plt.plot(x_new, f8(x_new), label=u"后点线性插值")
plt.legend()
plt.subplot(222)
plt.plot(x, y, "o", label=u"原始数据")
plt.plot(x_new, f1(x_new), label=u"线性插值")
plt.plot(x_new, f3(x_new), label=u"零阶样条插值")
plt.plot(x_new, f4(x_new), label=u"一阶样条插值")
plt.legend()
plt.subplot(223)
plt.plot(x, y, "o", label=u"原始数据")
plt.plot(x_new, f1(x_new), label=u"线性插值")
plt.plot(x_new, f5(x_new), label=u"三阶样条插值")
plt.legend()
plt.subplot(224)
plt.plot(x, y, "o", label=u"原始数据")
plt.plot(x_new, f1(x_new), label=u"线性插值")
plt.plot(x_new, f6(x_new), label=u"五阶样条插值")
plt.legend()
plt.show()不同的插值方法画在一起,对比一下效果会更明显:
2、二维插值
二维数据通常总是对应一个网格,例如经纬度网格。如果插值对象只有一个二维数组,那么我们可以使用数组的行列号来构造网格。
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['FangSong']
plt.rcParams['axes.unicode_minus'] = False
y, x = np.mgrid[-2:2:20j,-3:3:30j] # 30x20 = 600
z = x*np.exp(-x**2-y**2)
y_new, x_new = np.mgrid[-2:2:80j,-3:3:120j] # 120x80 = 9600
f1 = interpolate.interp2d(x[0,:], y[:,0], z, kind='linear') # 线性插值
f2 = interpolate.interp2d(x[0,:], y[:,0], z, kind='cubic') # 三阶样条
f3 = interpolate.interp2d(x[0,:], y[:,0], z, kind='quintic') # 五阶样条
z1 = f1(x_new[0,:], y_new[:,0])
z2 = f2(x_new[0,:], y_new[:,0])
z3 = f3(x_new[0,:], y_new[:,0])
plt.subplot(221)
plt.pcolor(x, y, z, cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')
plt.subplot(222)
plt.pcolor(x_new, y_new, z1, cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')
plt.subplot(223)
plt.pcolor(x_new, y_new, z2, cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')
plt.subplot(224)
plt.pcolor(x_new, y_new, z3, cmap=plt.cm.hsv)
plt.colorbar()
plt.axis('equal')
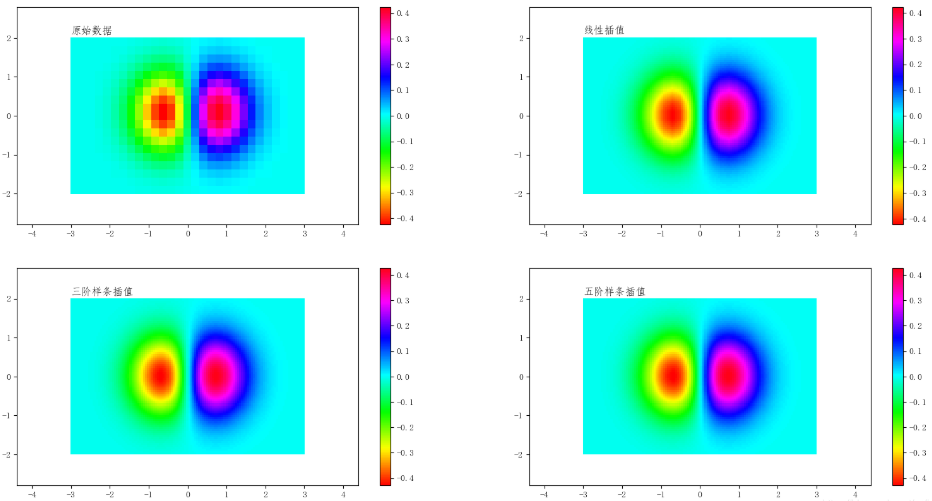
plt.show()原始数据、线性插值数据、三阶插值数据、五阶插值数据的效果对比如下:
二、拟合
在我们的工作中,我们经常需要用曲线来拟合实际数据,同时在图形中描绘一些实际的数据观察。所谓拟合就是找出符合数据变化趋势的曲线方程,进而对变化趋势进行预测。
1、使用numpy.polyfit拟合
numpy.polyfit() 实现最小二乘法。它的作用是返回指定次数的多项式参数。这组参数最小化了多项式和样本数据之间的误差。下面的代码虚拟化了谷神星的一段观测数据,并使用最小二乘法实现多项式拟合,进而推断出谷神星的未来轨迹。最后,将其与虚拟轨道方程进行比较。
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['FangSong']
plt.rcParams['axes.unicode_minus'] = False
def f(t):
"""谷神星虚拟的运行轨道方程。我们假装不知道,仅用来验证预测结果是否准确"""
t = t/7.5 -1
return ((t**2-1)**3 + 0.5)*np.sin(2*t)
t = np.linspace(0, 20, 201) # 用于绘制实际的运行轨迹线
_x = np.linspace(0, 15, 16) # 观测数据时间序列
_y = f(_x) # 观测数据位置序列
x = np.linspace(15, 20, 6) # 待预测的时间序列
loss_list = list()
for i in range(2,16): # 从2次到15次多项式,逐一计算误差
args = np.polyfit(_x, _y, i) # 用最小二乘法找到一组系数
g = np.poly1d(args) # 用这组系数生成方程g(x)
loss = np.sum(np.square(g(_x)-_y)) # 计算i次多项式拟合的误差
loss_list.append(loss)
print(i, loss)
k = loss_list.index(min(loss_list))+2
args = np.polyfit(_x, _y, k)
g = np.poly1d(args)
plt.figure('demo', facecolor='#eaeaea')
plt.plot(_x, _y, c='r', ls='', marker='o', label=u'观测数据')
plt.plot(_x, g(_x), c='b', ls='-', label=u'%d次多项式拟合,误差%0.8f'%(k, loss_list[k-2]))
plt.plot(x, g(x), c='r', ls=':', label=u'预测轨迹')
plt.plot(t, f(t), c='#60f0f0', ls='--', label=u'实际运行轨迹')
plt.legend(loc='lower left')
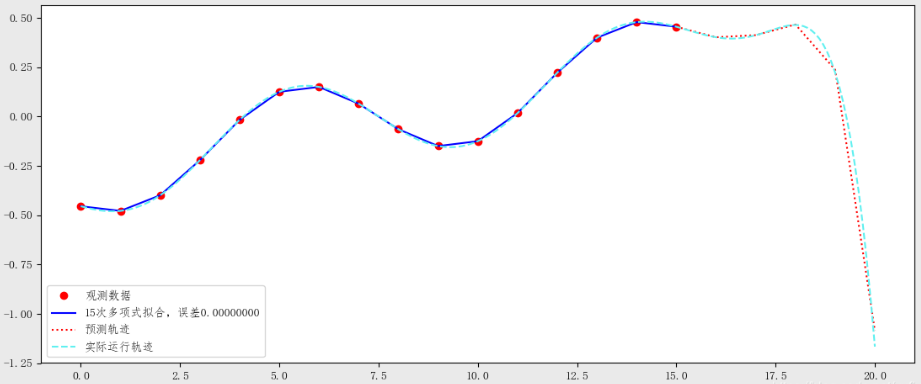
plt.show()把虚拟轨道、虚拟观测数据、拟合曲线和预测曲线画在一起,效果如下:
2、使用scipy.optimize.optimize.curve_fit拟合
不管曲线实际是什么样子,多项式拟合总是用有限次数的多项式来近似数据样本。还有一种拟合,就是我们知道曲线的标准方程,但是有些系数或者参数是不确定的。这种拟合也是为了找到最好的系数或参数。 scipy提供的拟合需要先确定带参数的曲线方程,然后用scipy求解方程,返回曲线参数。
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import optimize
>>> x = np.arange(1,13,1)
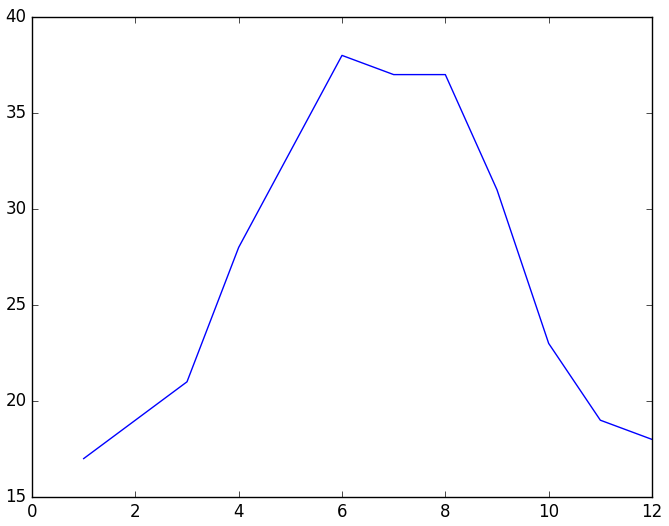
>>> y = np.array([17,19,21,28,33,38,37,37,31,23,19,18 ])
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x04799D10>]
>>> plt.show()可以看出,曲线近似正弦函数。构造函数y=asin(xpi/6+b)+c,使用scipy的optimize.curve_fit函数求a、b、c的值:
>>> def fmax(x,a,b,c):
return a*np.sin(x*np.pi/6+b)+c
>>> fita, fitb = optimize.curve_fit(fmax, x, y, [1,1,1])
>>> print fita
[ 10.93254951 -1.9496096 26.75 ]
>>> xn = np.arange(1,13,0.1)
>>> plt.plot(x, y)
[<matplotlib.lines.Line2D object at 0x04B160B0>]
>>> plt.plot(xn, fmax(xn, fita[0],fita[1],fita[2]))
[<matplotlib.lines.Line2D object at 0x04B16510>]
>>> plt.show()
三、求解非线性方程(组)
在数学建模中,需要求解一些奇怪的方程(组)。 Matlab自然是首选,但是Matlab不是免费的,而scipy为我们提供了免费的午餐! scipy.optimize 库中的 fsolve 函数可用于求解非线性方程(系统)。它的基本调用形式如下:
fsolve(func, x0)func(x) 是计算方程组误差的函数。它的参数 x 是一个向量,表示方程组中每个未知数的一组可能解。 func 返回将 x 代入方程组后得到的误差; x0 是未知值向量的初始值。
我们先来求解一个简单的方程:$ \sin(x) - \cos(x) = 0.2$
>>> from scipy.optimize import fsolve
>>> import numpy as np
>>> def f(A):
x = float(A[0])
return [np.sin(x) - np.cos(x) - 0.2]
>>> result = fsolve(f, [1])
array([ 0.92729522])
>>> print result
[0.92729522]
>>> print f(result)
[2.7977428707082197e-09]哈哈,易如反掌!再来一个方程组:
>>> from scipy.optimize import fsolve
>>> import numpy as np
>>> def f(A):
x = float(A[0])
y = float(A[1])
z = float(A[2])
return [4*x*x - 2*np.sin(y*z), 5*y + 3, y*z - 1.5]
>>> result = fsolve(f, [1, 1, 1])
>>> print result
[-0.70622057 -0.6 -2.5 ]
>>> print f(result)
[-9.1260332624187868e-14, 0.0, 5.329070518200751e-15]
四、数值积分
数值积分是定积分的数值解。例如,数值积分可以用来计算某个形状的面积。我们知道,半径为1的圆的方程可以写成:
现在让我们考虑如何计算一个半径为1的半圆的面积。根据圆的面积公式,它的面积应该等于PI/2。单位半圆曲线可以用以下函数表示:
我们先定义一个计算根据x计算y的函数:
>>> def half_circle(x):
return (1-x**2)**0.5
1、经典微分法
下面的程序使用经典的计算小矩形面积和的方法来计算一个单位半圆的面积:
>>> N = 10000
>>> x = np.linspace(-1, 1, N)
>>> dx = 2.0/N
>>> y = half_circle(x)
>>> dx * np.sum(y[:-1] + y[1:]) # 面积的两倍
3.1412751679988937
2、使用定积分求解函数
如果我们调用 scipy.integrate 库中的 quad 函数,我们将得到非常准确的结果:
>>> from scipy import integrate
>>> pi_half, err = integrate.quad(half_circle, -1, 1)
>>> pi_half*2
3.1415926535897984
五、图像处理
在 scipy.misc 模块中,有一个加载 Lena 图像的函数——该图像是用于图像处理的经典演示图像。我只是简要地展示了这张图片上的一些操作。
(1)载入Lena图像,并显示灰度图像
(2) 应用中值滤波器扫描信号的每个数据点,并用相邻数据点的中值代替
(3)旋转图像
(4)应用Prewitt滤波器(基于图像强度的梯度计算)
>>> from scipy import misc
>>> from scipy import ndimage
>>> img = misc.lena().astype(np.float32)
>>> plt.subplot(221)
>>> plt.title('Original Image')
>>> plt.imshow(img, cmap=plt.cm.gray)
>>> plt.subplot(222)
>>> plt.title('Median Filter')
>>> filtered = ndimage.median_filter(img, size=(42,42))
>>> plt.imshow(filtered, cmap=plt.cm.gray)
>>> plt.subplot(223)
>>> plt.title('Rotated')
>>> rotated = ndimage.rotate(img, 90)
>>> plt.imshow(rotated, cmap=plt.cm.gray)
>>> plt.subplot(224)
>>> plt.title('Prewitt Filter')
>>> filtered = ndimage.prewitt(img)
>>> plt.imshow(filtered, cmap=plt.cm.gray)
>>> plt.show()
python学习网,大量的免费
,欢迎在线学习!
1、
2、
本文为原创文章,版权归知行编程网所有,欢迎分享本文,转载请保留出处!
你可能也喜欢
- ♥ python中设置了什么09/02
- ♥ 你了解python单例模式吗?12/22
- ♥ python如何随机生成一堆数字并输出10/21
- ♥ 如何在python中表示换行符09/07
- ♥ 如何使用python操作文件目录?哪些方法?01/04
- ♥ Python中的对象序列化和反序列化方法01/01





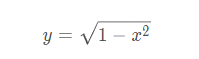


内容反馈