你知道 Python 中的树吗？

树与二叉树

在了解二叉树之前，我们需要了解一下树的一些概念，以方便我们对二叉树的理解。

什么是树？

树（英文：tree）是一种抽象数据类型（abstract data type，ADT）或实现这种抽象数据类型的数据结构，用来模拟具有树状结构的数据集。

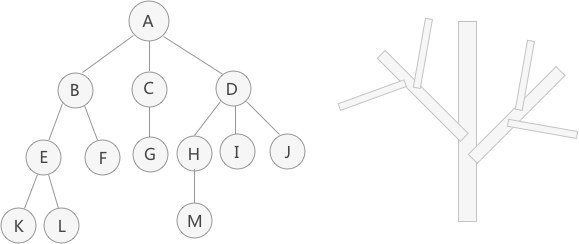
它由n（n>=1）个有限节点组成一个具有层次关系的集合。之所以称为“树”，是因为它看起来像一棵倒挂的树，即根朝上，叶子朝下。它具有以下特点：

每个节点有零个或多个子节点;

没有父节点的节点称为根节点;

每一个非根节点有且只有一个父节点;

除了根节点，每个子节点还可以分成多个不相交的子树；

树的术语：

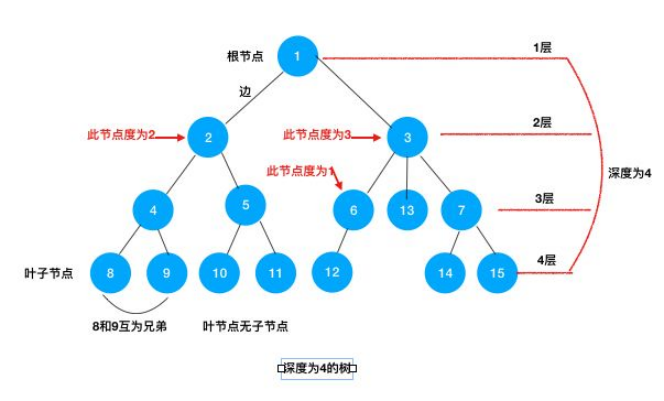
节点的度：一个节点包含的子树的个数，称为该节点的度；

树的度: 一棵树中,节点的度称为树的度;

根节点：树的最顶层节点，继续划分子节点

父节点： 子节点的上一层为父节点

兄弟节点：具有相同父节点的节点称为兄弟节点

叶节点/终端节点：不再有孩子的节点是叶节点

二叉树：

二叉树是树的特殊一种，具有如下特点：

每个节点最多有两个子树，节点的度为2

左子树和右子树是有顺序的，次序不能颠倒

即是某节点只有一个子树，也要区分左右子树

二叉树的性质：

在非空二叉树的第i层，最多有2i-1个节点(i>=1)

在深度为K的二叉树上最多有2k-1个节点(k>.1)

对于任何非空二叉树，如果叶子节点的个数为n0，度为2的节点个数为n2，则n0=n2+1

下推过程：在一棵二叉树中，除了叶子节点（0度），只有度数为2（n2）和度数为1（n1）的节点。那么树的节点总数为T = n0 + n1 + n2；二叉树的总节点数为T，总连接数为T-1 = 2*n2 + n1，所以有：n0 + n1 + n2 - 1 = 2 *n2 + n1，得n0= n2+1。

特殊的二叉树

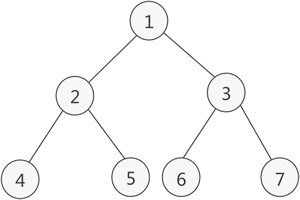
满二叉树

在一棵二叉树中，除叶子节点外，其他所有节点的度数均为2，且所有叶子节点都在同一层，这样的二叉树就成为满二叉树。

满二叉树的特点：

叶子节点只能出现在最下一层

非叶子节点度数一定为2

相同深度的二叉树中，满二叉树的节点数最多，叶子节点数最多

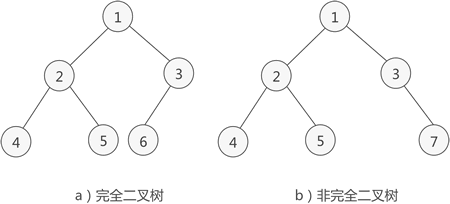
完全二叉树

如果二叉树去掉最后一层叶子节点后​​是一棵满二叉树，并且最后一层的叶子节点从左到右依次分布，那么这样的二叉树就称为完全二叉树

完全二叉树的特点：

叶子节点一般出现在底层。如果叶子节点出现在倒数第二层，则必须出现在右侧连续的位置

最下层叶子节点一定集中在左部连续位置

同一个结点的二叉树，完全二叉树的深度最小（完全二叉树也是正确的）

小例题：

一棵完全二叉树有200个节点，二叉树有()个叶子节点？

解：n0+n1+n2=200，其中n0=n2+1，n1=0或1（n1=1，底层出现的节点数为奇数，底层出现的节点数是偶数，则n1=0)，因为n0是整数，所以最终n0=100。

完全二叉树的性质：

具有 n 个节点的完全二叉树的深度为 log2n+1。 log2n 结果的整数部分。

如果有一棵有n个节点的完全二叉树，节点按层级顺序编号，对于节点i(1 <= i <= n)的任意一层

1、如果i=1，则该节点是二叉树的根节点，没有父节点。如果i>1，其父节点为i/2，向下取整

2. 如果2*1>n，那么节点i没有左孩子，否则其左孩子为2i

3. 如果2i+1>n那么节点没有右孩子，否则右孩子为2i+1

验证：

第一条：

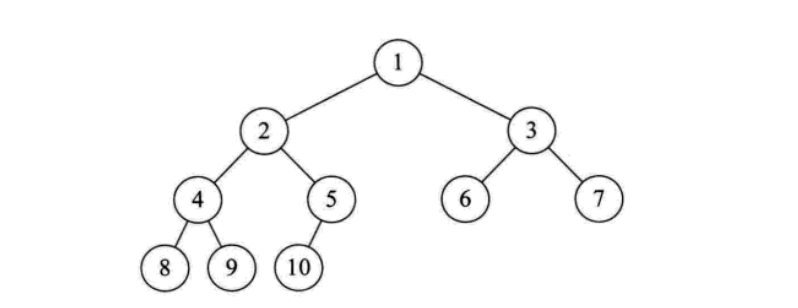
i=1时为根节点。当i>1时，例如节点为7，其父节点为7/2=3；节点 9 的父节点是 4。

第二条：

节点6,62 = 12>10，所以节点6没有左孩子，是叶子节点。节点5，52 = 10，左孩子为10，节点4为8。

第三条：

结点5，2*5+1>10,没有右孩子，结点4，则有右孩子。

更多Python相关知识，请移步
继续学习！！