python图形含义

Graph - 算法中最强大的框架之一。树结构只是图的一种特殊情况。

如果我们可以将我们的工作解释为图形问题，那么该问题至少接近于解决方案。而我们的问题实例可以用树形结构（树）来解释，那么我们基本上就有了一个真正有效的解决方案。

邻接表及加权邻接字典

实现图结构最直观的方法之一是使用邻接表。基本上为每个节点设置一个邻接列表。让我们实现最简单的一个：假设我们有 n 个节点，编号为 0，...，n-1。

一个节点当然可以是任何对象，并且可以被赋予任何标签或名称。但是使用区间 0, ..., n-1 中的整数来实现要简单得多。因为如果我们可以用数字来表示节点，那么我们索引显然要容易很多。

那么每个邻接（邻居）列表只是一个数字列表，我们可以将它们分组到一个大小为 n 的主列表中，并通过节点编号对其进行索引。由于这些列表中节点的顺序是任意的，因此我们实际上是使用列表来实现邻接集。术语列表在这里仍然使用主要是因为传统。幸运的是，Python 本身提供了一个单独的集合类型。

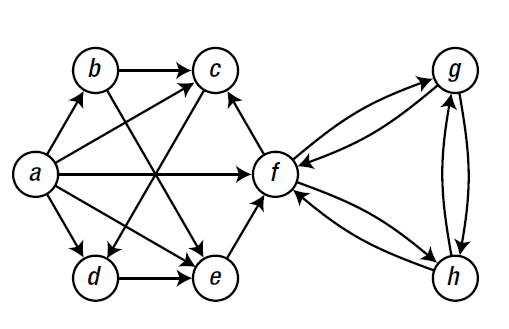
我们以下图为例来说明图结构的各种表示方法（当我们在做图相关的工作时，需要反复遵循一个主题，即表示图的最佳方式应该取决于我们想要做什么）它是什么）：

a, b, c, d, e, f, g, h = range(8)
N = [
  {b, c, d, e, f},
  {c, e},
  {d},
  {e},
  {f},
  {c, g, h},
  {f, h},
  {f, g}
]

在图论中，N(v) 代表的是 v 的邻居节点集；

>>> b in N[a] # neighborhood membership
True
>>> len(N[f]) # out-degree：出度
3

加权邻接字典

使用 dict 类型而不是 set 或 list 来表示邻接集。在 dict 类型中，每个邻居节点都会有一个 key 和一个额外的 value 来表示其邻居节点（或出边）之间的关联，例如边的权重。

a, b, c, d, e, f, g, h = range(8)
N = [
  {b:2, c:1, d:3, e:9, f:4},
  {c:4, e:4},
  {d:8},
  {e:7},
  {f:5},
  {c:2, g:2, h:2},
  {f:1, h:6},
  {f:9, g:8}
]

客户端调用：

>>> b in N[a]         # neighborhood membership
True
>>> len(N[f])         # out-degree
3
>>> N[a][b]          # Edge weight for (a, b)
2

邻接矩阵

邻接矩阵是图的另一种表示，这种表示的主要区别在于它不再列出每个节点的所有邻居节点。

a, b, c, d, e, f, g, h = range(8)
N =[
  [0, 1, 1, 1, 1, 1, 0, 0],
  [0, 0, 1, 0, 1, 0, 0, 0],
  [0, 0, 0, 1, 0, 0, 0, 0],
  [0, 0, 0, 0, 1, 0, 0, 0],
  [0, 0, 0, 0, 0, 1, 0, 0],
  [0, 0, 1, 0, 0, 0, 1, 1],
  [0, 0, 0, 0, 0, 1, 0, 1],
  [0, 0, 0, 0, 0, 1, 1, 0],
]

关于邻接矩阵：

（1）主对角线为自己到自己，为0

（2）行和为出度

（3）列和为入度