二叉排序树
二叉排序树也称为二叉搜索树。它要么是一棵空树,要么是具有以下属性的二叉树:
若它的左子树不为空,则左子树上所有节点的值均小于它的根结构的值;若它的右子树不为空,则右子树上所有节点的值均大于它的根结构的值;它的左、右子树也分别为二叉排序树。
构造二叉排序树的目的往往不是为了排序,而是提高搜索和插入删除关键字的速度。
二叉排序树的操作:
搜索:比较节点的值和关键字,如果相等,表示已经找到;如果较小,则去节点的左子树,如果较大,则去右子树,以此类推,最后返回布尔值或找到的节点。插入:从根节点开始,与关键字一一比较,小则向左,大则向右,子树为空时链接新节点。删除:如果要删除的节点是叶子,直接删除;如果只有左子树或只有右子树,删除节点后,将子树链接到父节点;如果同时存在左右子树,则可以删除这两个叉排序树进行中序遍历,取待删除节点的前驱或后继替换被删除节点的位置。
"""
定义一个二叉树节点类。
以讨论算法为主,忽略了一些诸如对数据类型进行判断的问题。
"""
def __init__(self, data, left=None, right=None):
"""
初始化
:param data: 节点储存的数据
:param left: 节点左子树
:param right: 节点右子树
"""
self.data = data
self.left = left
self.right = rightclass BinarySortTree:
"""
基于BSTNode类的二叉排序树。维护一个根节点的指针。
"""
def __init__(self):
self._root = None
def is_empty(self):
return self._root is None
def search(self, key):
"""
关键码检索
:param key: 关键码
:return: 查询节点或None
"""
bt = self._root while bt:
entry = bt.data if key < entry:
bt = bt.left elif key > entry:
bt = bt.right else: return entry return None
def insert(self, key):
"""
插入操作
:param key:关键码
:return: 布尔值
"""
bt = self._root if not bt:
self._root = BSTNode(key) return
while True:
entry = bt.data if key < entry: if bt.left is None:
bt.left = BSTNode(key) return
bt = bt.left elif key > entry: if bt.right is None:
bt.right = BSTNode(key) return
bt = bt.right else:
bt.data = key return
def delete(self, key):
"""
二叉排序树最复杂的方法
:param key: 关键码
:return: 布尔值
"""
p, q = None, self._root # 维持p为q的父节点,用于后面的链接操作
if not q:
print("空树!") return
while q and q.data != key:
p = q if key < q.data:
q = q.left else:
q = q.right if not q: # 当树中没有关键码key时,结束退出。
return
# 上面已将找到了要删除的节点,用q引用。而p则是q的父节点或者None(q为根节点时)。
if not q.left: if p is None:
self._root = q.right elif q is p.left:
p.left = q.right else:
p.right = q.right return
# 查找节点q的左子树的最右节点,将q的右子树链接为该节点的右子树
# 该方法可能会增大树的深度,效率并不算高。可以设计其它的方法。
r = q.left while r.right:
r = r.right
r.right = q.right if p is None:
self._root = q.left elif p.left is q:
p.left = q.left else:
p.right = q.left def __iter__(self):
"""
实现二叉树的中序遍历算法,
展示我们创建的二叉排序树.
直接使用python内置的列表作为一个栈。
:return: data
"""
stack = []
node = self._root while node or stack: while node:
stack.append(node)
node = node.left
node = stack.pop() yield node.data
node = node.rightif __name__ == '__main__':
lis = [62, 58, 88, 48, 73, 99, 35, 51, 93, 29, 37, 49, 56, 36, 50]
bs_tree = BinarySortTree() for i in range(len(lis)):
bs_tree.insert(lis[i]) # bs_tree.insert(100)
bs_tree.delete(58) for i in bs_tree:
print(i, end=" ") # print("\n", bs_tree.search(4))
二叉排序树总结:
二叉排序树采用链式存储,保持了链式结构的优点,用于插入和删除操作。在极端情况下,查询次数为 1,但操作次数不会超过树的深度。也就是说,二叉排序树的搜索性能取决于二叉排序树的形状,从而导致下面的平衡二叉树。给定一组元素,可以构造不同的二叉排序树。当它也是完全二叉树时,查找的时间复杂度为O(log(n)),类似于二叉查找。当出现最极端的斜树时,其时间复杂度为O(n),相当于顺序搜索,效果最差。
平衡二叉树
平衡二叉树(AVL树,发明人姓名缩写):高度平衡的排序二叉树,其中每个节点的左右子树的高度差最多为1。
平衡二叉树首先必须是一棵二叉排序树!
平衡因子:二叉树上节点的左子树深度减去右子树深度的值。
对于一棵平衡二叉树,包括分支节点和叶子节点在内的所有平衡因子只能是-1、0和1。只要一个节点的因子不在这三个值之内,二叉树就是不平衡的。
最小不平衡子树:以离插入节点最近的节点为根且平衡因子绝对值大于1的子树。
平衡二叉树的构造思想:每当插入一个新节点时,首先检查树的平衡是否被破坏,如果是,则找到最小的不平衡子树。在保持二叉排序树特性的前提下,调整最小不平衡子树中节点之间的连接关系,并进行相应的旋转,成为新的平衡子树。
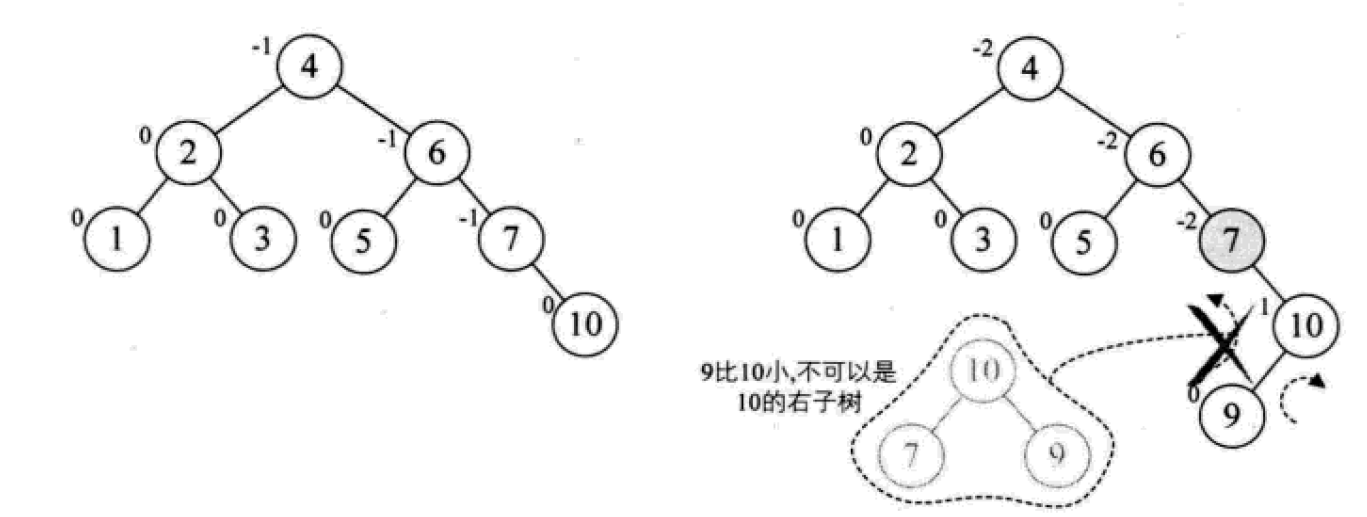
下面是由[1,2,3,4,5,6,7,10,9]构建平衡二叉树
本文为原创文章,版权归知行编程网所有,欢迎分享本文,转载请保留出处!













内容反馈