一、箱线图概念
箱线图,也称为箱线图、箱线图或箱线图,是一种统计图表,用于显示有关一组数据的离散度信息。
计算过程:
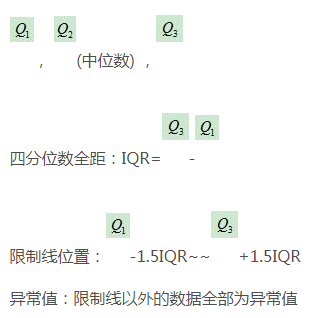
(1)计算上四分位数(Q3),中位数,下四分位数(Q1)
(2)计算上四分位数和下四分位数的差值,即四分位数差(IQR,四分位距)Q3-Q1
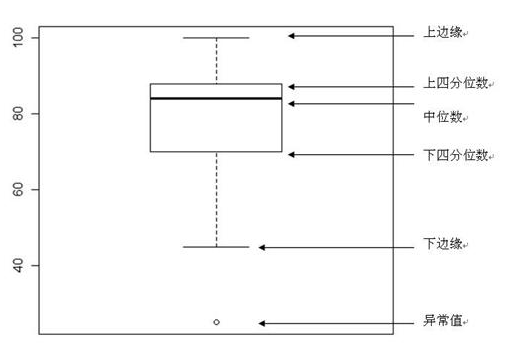
(3)绘制箱线图的上下范围,上限为上四分位数,下限为下四分位数。在方框内中线的位置画一条水平线。
(4) 大于上四分位数四分位差的1.5倍,或小于下四分位数四分位差1.5倍的值,归类为异常值。
(5)在离群点外,在最接近上下边缘的两个值处画水平线作为箱线图的胡须。
(6)极端异常值,即超过四分位差3倍的异常值,用实心点表示;较温和的异常值,即四分位差值在 1.5 倍到 3 倍之间的异常值,用空心圆点表示。
(7)为箱线图添加名称,数轴等。
二、四分位数的计算
分位数可以分为中位数、四分位数、十分位数、百分位数等。四分位数作为分位数的一种形式,在统计学中起着非常重要的作用,而关于统计学原理的教科书大多只介绍它的基本含义,以及它的具体计算方法。 ,尤其是组区间序列的计算没有做介绍,成为统计原理教科书中的空白。那么,如何从数字序列中计算四分位数呢?一般来说,这取决于数据是否分组。
1、根据未分组的资料计算四分位数
第一步:确定四分位数的位置
第二步:根据第一步确定的四分位数的位置确定对应的四分位数。
例1:某车间某工人某月生产某产品的数量为13、13.5、13.8、13.9、14、14.6、14.8、15、15.2、15.4、15.7公斤,三个四分位数的位置是 :
即变量数列中的第三个、第六个、第九个工人的某种产品产量分别为下四分位数、中位 数和上四分位数。即:
Q1 =13.8公斤、Q2=14.6公斤、Q3=15.2公斤
在上面的例子中 (n+1) 正好是 4 的倍数,所以更容易确定四分位数。如果 (n+1) 不是 4 的整数倍,则上述分数计算出来的四分位数位置会有小数,此时相关四分位数应该是相邻两个整数位置的标志值的平均值小数点。权重的大小取决于两个整数位置之间的距离。距离越近,重量越大。数字越大,距离越远,权重越小,权重之和等于1。
例2:某车间某月某工人生产某产品的数量为13、13.5、13.8、13.9、14、14.6、14.8、15、15.2、15.4kg,则三个四分位数的位置为:
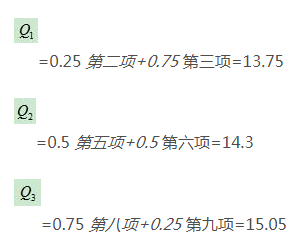
即变量序列中的第2.75、5.5、8.25项分别为下四分位数、中位数和上四分位数。这是:
在实际数据中,由于标记值序列中相邻的标记值往往是相同的,因此不需要通过计算得到相关的四分位数。
2、由组距式数列确定四分位数
第一步,向上或向下累计次数.
第二步,根据累计次数确定四分位数的位置.
(1)当四分位数由向上累积次数的数据确定时,四分位数位置的计算公式为:
(2)当四分位数采用向下累计次数数据确定时,四分位数位置的计算公式为:
第三步,根据四分位数的位置算出各四分位数.
(1)累计次数向上时,按下限公式计算四分位数。
(2)、当累计次数是向下累计时,按上限公式计算各四分位数.
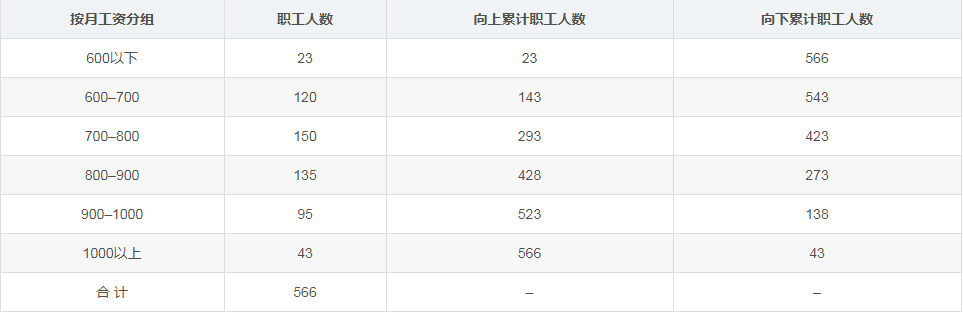
例3:某企业职工按月工资的分组资料如下:
基于以上信息,确定企业职工月工资四分之三如下:
(1) 使用向上累计员工数数据得到的月工资四分位数位置为:
(2) 使用向下累计员工数得到的月薪四分位数的位置为:
3、异常值
三、画图
# Python
import plotly.plotly
import plotly.graph_objs as go
data = [
go.Box(
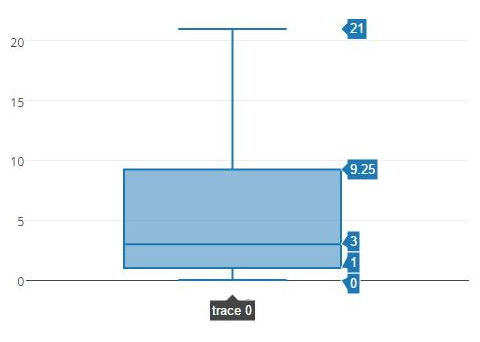
y=[0, 1, 1, 2, 3, 5, 8, 13, 21] # 9个数据
)
]
plotly.offline.plot(data) # 离线绘图本文为原创文章,版权归知行编程网所有,欢迎分享本文,转载请保留出处!



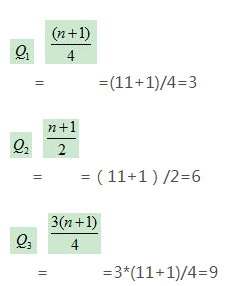
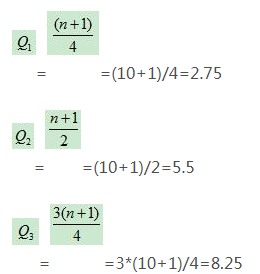
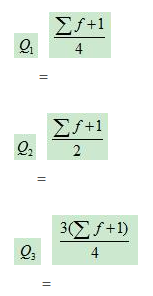
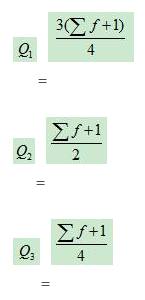
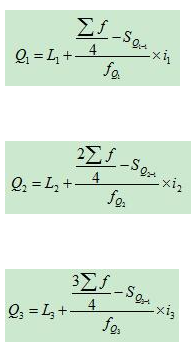
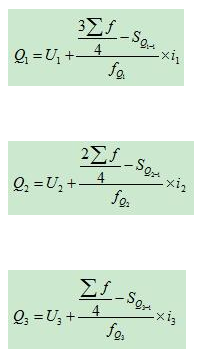


内容反馈