Python中美丽星空代码详解！

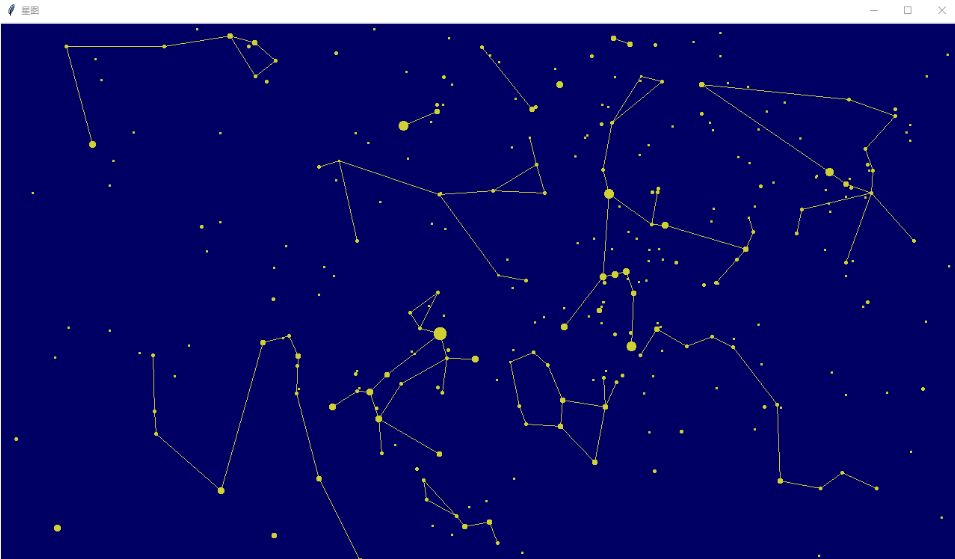
用Python显示真实的星空

还是先上图

本文讲怎样画出真实的星空。

预备知识

如果想显示真实的星空，首先你得有真实恒星的位置坐标和亮度标记。它的基本格式如下：
{'long': 0.023278328898474372, 'lat': -0.09961466705757636, 'light': 46, 'const': 66},
{'long': 0.024870941840919196, 'lat': 0.2338062439126301, 'light': 55, 'const': 62},
{'long': 0.028107061526797, 'lat': 1.1204335039257496, 'light': 56, 'const': 18},
{'long': 0.03660100303760025, 'lat': 0.5077259659824991, 'light': 21, 'const': 1},
{'long': 0.04004802831028905, 'lat': 1.0323574005393255, 'light': 23, 'const': 18},
{'long': 0.03944444109507185, 'lat': 0.3178583859888262, 'light': 55, 'const': 62},
{'long': 0.040797071265367454, 'lat': -0.488478858963941, 'light': 54, 'const': 74},
{'long': 0.0410661312228549, 'lat': -0.798444499556106, 'light': 39, 'const': 64},
{'long': 0.043800486202076855, 'lat': 0.1945266317121166, 'light': 55, 'const': 66},
{'long': 0.045036755271142, 'lat': 0.804111967609767, 'light': 50, 'const': 1},
{'long': 0.043785947609407745, 'lat': -1.4350775693910554, 'light': 53, 'const': 58},
{'long': 0.04915283505929031, 'lat': -0.2699684886295715, 'light': 49, 'const': 21},
{'long': 0.050498187206605094, 'lat': -0.4851966800391031, 'light': 54, 'const': 74},

每颗恒星包含4条信息：天经长、天纬纬度、亮度光（越小越亮）、所属星座。

想象一下，所有的星星都嵌在一个天球中，而且它们的位置是固定的，所以它们被称为星星。

星星的坐标用纬度和经度表示，就像地球上的位置用纬度和经度表示一样。当地球自转时，我们看到天球的自转。

正如我们所知，北极星非常靠近天球的北极。

在天球自转过程中，它的位置几乎没有移动。这意味着北极星的位置几乎始终保持在天空中的固定位置。之所以能用北极星来指示方向，就是这个原理。

此外，星空是球形的。要将其显示在屏幕上，涉及到几组基本参数的设置：

观测地的经纬度

观测的日期和时间

观测者的观测角度和屏幕大小

在这几组参数中，关系如下：观测点的维度是第一位的，观测点确定后，可以看到的星空（天球的倾角）就确定了，所有的星星只有在赤道上才能看到，在其他空间会有一些看不到的星星。

在最极端的情况下，在两极，总是只能看到天球的一半（即恒星数量的一半）。

观测点的经度、观测日期和观测时间其实是等价的，因为地球的公转和自转可以认为与遥远的星空没有区别。

当观测点和观测日期和时间确定后，理论上可以认为能看到的星空大约是整个天空中星星的一半。但是屏幕上能显示的星星取决于你看的地方和屏幕有多大。

如果你能理解以上基础知识，请继续阅读。

星空计算

计算经过这样几个步骤：

1、为了方便计算，先将每颗恒星的经纬度转换成xyz的三维坐标。在这个过渡过程中，我们看到一个直立的天球，北极向上，南极向下。

2、将观测地的纬度引入每颗计算

3、将观测地点的经度、观测日期、观测时间组合起来，形成经度数据，在每次计算中引入

4、将观测者的朝向引入每颗计算

5、将观测者的仰角引入每颗计算

6、向屏幕投影

代码如下：

def calcStar(stars,Long,Lat,winLong,winLat,eyeDistant):
    Long= radians(Long)
    Lat= radians(Lat)
    winLong= radians(winLong)
    winLat= radians(winLat)
    for star in stars:
        # print(star)
        # 经纬度转换为xyz的三维坐标
        x0= cos(star['long'])* cos(star['lat'])
        y0= sin(star['long'])* cos(star['lat'])
        z0= sin(star['lat'])
        # 观测地经度及日期时间的合并
        x1= x0*cos(Long)- y0*sin(Long)
        y1= x0*sin(Long)+ y0*cos(Long)
        z1= z0
        # 观测地纬度
        x2= x1* sin(Lat)- z1* cos(Lat)
        y2= y1;
        z2= x1* cos(Lat)+ z1* sin(Lat)
        # 观测者转身
        x3= x2* cos(winLong)+ y2* sin(winLong)
        y3= -x2* sin(winLong)+ y2* cos(winLong)
        z3= z2
        # 观测者俯仰
        x4= x3* sin(winLat)- z3* cos(winLat)
        y4= y3
        z4= x3* cos(winLat)+ z3* sin(winLat)
        # 屏幕投影
        star['visible']= (z2> 0 and z4>0)
        star['x']= x4* eyeDistant/z4
        star['y']= y4* eyeDistant/z4
        star['z']= z4

一颗星星在地平线以上（z2>0）且在观察者前方（z4>0）是可见的，而可见的星星是否实际显示在屏幕上取决于它是否在屏幕显示范围内。

显示代码如下：

img= Image.new('RGBA', (1280,720), (0,0,120,255))  # 深蓝色天空
draw = ImageDraw.Draw(img)
color= (255,255,0,255)    # 黄色星星
for star in stars:
    # 屏幕中心
    x= round(-star['y']+ 640)
    y= round(star['x']+ 360)
    # 亮度值越小越亮，这里用大小来表示
    r= round(6-star['light']/10)    
    if visible(star):
        # print(x,y)
        draw.ellipse((x-r, y-r, x+r, y+r), fill=color)
img.show()

怎样将经度、观测日期和观测时间结合起来

这个问题比想象的要复杂得多。要想真正准确，会涉及到平太阳日、真太阳日、恒星日、岁差、经度与当地时间的时差等诸多细节。

幸运的是，这些错误并不算大。如果你的目标不是科学研究，只考虑现代性而不考虑古代和未来，那么一些错误即使忽略也不会有太大影响。

这里我使用一个简单但足够准确的经验公式来计算。输入观测地点的经度，观测的日期和时间，返回一个所谓的绝对经度，作为我们用来计算恒星位置的经度值。

代码如下：

def getAbsLong(aLong, ayy, amm, add, ahh, amin):
    # 年的影响忽略
    # 月日的影响，首先计算太阳赤经
    # 春分点3月21日为经度0，一年平均365.25天，旋转360度，用插值方法简单计算
    a= julianDay(ayy, amm, add)    
    b= julianDay(ayy, 3, 21)
    v= 0- (a-b)/365.25*360
    # 因为使用本地时间，基本可以忽略经度+时区的影响（互相抵消）
    # 时分的影响，中午12点，正对太阳赤经，一天24小时，旋转360度，用插值简单计算
    c= ahh*60+amin
    d= 12*60
    v= v- (c-d)/(24*60)*360
    return v

星座连线是怎么来的

星座线是用来帮助我们理解星座形状的。结构很简单，就是表示哪两个点与一条线相关联。此处不展开，详情见代码。

{'star1': 61, 'star2': 4, 'const': 1},
{'star1': 60, 'star2': 61, 'const': 1},
{'star1': 83, 'star2': 60, 'const': 1},
{'star1': 83, 'star2': 109, 'const': 1},
{'star1': 61, 'star2': 58, 'const': 1},
{'star1': 58, 'star2': 22, 'const': 1},
{'star1': 22, 'star2': 3097, 'const': 1},
{'star1': 3097, 'star2': 3097, 'const': 1},
{'star1': 3097, 'star2': 3088, 'const': 1},
{'star1': 3007, 'star2': 3090, 'const': 1},
{'star1': 142, 'star2': 61, 'const': 1},